探索勾股定理课件八上VIP免费

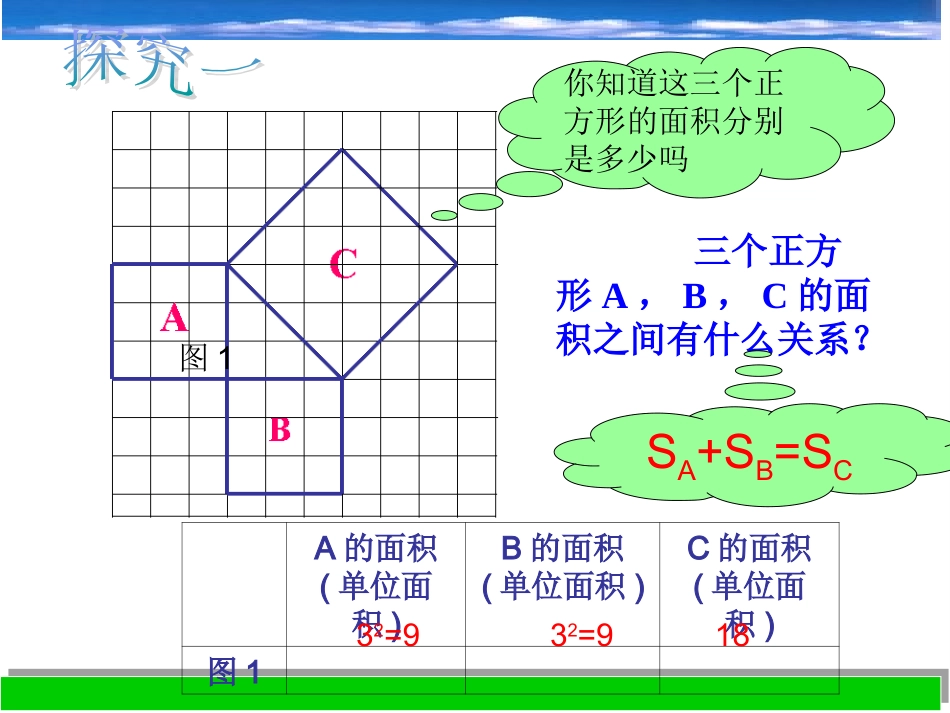
你能看出会徽与弦图之间的联系吗？2002年世界数学大会的会徽著名的“赵爽弦图”你知道这三个正方形的面积分别是多少吗图1三个正方形A，B，C的面积之间有什么关系？SA+SB=SCA的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图132=932=918ABC图222=4sA+sB=sC32=913ABCacbSa+Sb=Sc设：直角三角形的三边长分别是a、b、c猜想:两直角边a、b与斜边c之间的关系？a2+b2=c2┏a2+b2=c2acb直角三角形两直角边的平方和等于斜边的平方.勾股弦命题：在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.勾股勾股定理——千古第一定理在古代，许多民族发现了这个事实，即直角三角形的三条边长为a，b，c，则a2+b2=c2，其中a、b是直角边长，c是斜边长.在公元前2世纪，我国的数学著作《周髀算经》记着商高的一段话，意思是说：“把一直尺折断组成一个直角三角形，若勾为三，股为四，则弦为五”，即“勾三股四弦五”其中“勾”指的是较短的直角边，“股”是较长的直角边，“弦”是斜边。因此把这个定理命名为“勾股定理”或“商高定理”，在西方，被称为“毕达哥拉斯”定理。数学文化股勾弦读一读我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会（TCM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就.图1-1图1-2acbabc22214)(cabab222cba22222cabaabb思考：大正方形面积怎么求？赵爽弦图结论：┏a2+b2=c2acb直角三角形两直角边的平方和等于斜边的平方.勾股弦勾股定理做一做：P62540026xP的面积=______________X=____________24322622x24225BACAB=__________AC=__________BC=__________251520例1已知△ABC中,∠C=Rt∠,BC=a,AC=b,AB=c•已知:a=1,b=2,求c;•已知:a=15,c=17,求b;CABabc解:(1)根据勾股定理得:c2=a2+b2∵c>0,c=∴5=12+22=5(2)根据勾股定理得:∵b>0,b=8∴=172-152=64=(17＋15)(17－15)b2=c2-a21、如图：在Rt△ABC中,C=90∠°已知c＝13，a＝5，求b的值.练一练练一练cabBAC勾股定理的主要作用是：在直角三角形中,已知任意两边求第三边的长；已知一边及另两边的关系，求另两边。练一练练一练(1)a＝3，b＝4，则c=____.(2)c＝17，a＝8，则b=____.(3)c=61，b=60，则a=____.cabBAC(4)a:b＝3:4，c=10则a=____,b=____.5151168例2、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离。ABC409016040解:过A作铅垂线,过B作水平线,两线交于点C,则∠C=90。AC=90-40=50(mm),BC=160-40=120(mm).∵∠C=90。∴AB2=AC2+BC2∵AB>0∴AB=130(mm)答:两孔中心A,B之间的距离为130mm.温馨提示：在实际问题中，要会根据需要构造直角三角形，再通过勾股定理来解决问题。=502+1202=16900(mm2)如图，一块长约8m，宽约6m的长方形草地，被不自觉的人沿对角线踏出了一条斜“路”，类似的现象也时有发生.请问：①走斜“路”的客观原因是什么？②斜“路”比正路近多少？走这么几步近路，值得吗？68BCA勾股定理：直角三角形两直角边a，b的平方和，等于斜边为c的平方.即a2+b2=c2符号语言：如图：在Rt△ABC中,C=90∠°,则a2+b2=c2公式变形：a2=c2-b2c=b2=c2-a2a=b=小结勾股定理的主要用途是：在直角三角形中,1、已知任意两边求第三边的长；2、已知一边及另两边的关系，求另两边.cabBAC22ba22bc22ac勾弦股作业：1、作业本2、通过查阅资料，了解勾股定理的文化背景.3、通过查阅资料，了解勾股定理的证明方法.