反比例函数回顾与思考VIP免费

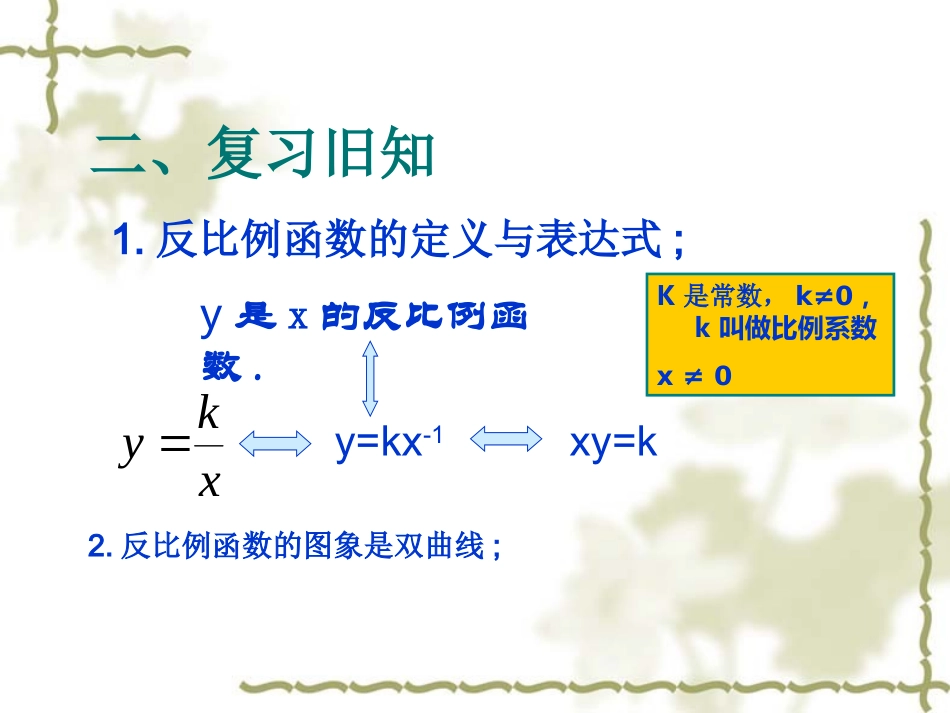
一、本章知识结构图现实世界中的反比例关系反比例函数实际应用反比例函数的图象和性质归纳二、复习旧知2.反比例函数的图象是双曲线;1.反比例函数的定义与表达式;y=kx-1xy=ky是x的反比例函数.xkyK是常数，k≠0，k叫做比例系数x≠03.在一个反比例函数图象上任取两点P，Q，过点P，Q分别作x、轴，y轴的平行线，与坐标轴围成的矩形面积为，,则和有何关系？xkykSS214.反比例函数既是中心对称图形，又是轴对称图形。1S2S1S2SP(m,n)AoyxBP(m,n)AoyxB面积性质（一）（1）过点P分别作x轴，y轴的垂线，垂足为A，B，则S矩形OAPB=OA.AP=|m|.|n|=|k|.有上任意一点是双曲线设:,)0(),(kxkynmP||21||||2121knmAPOASOAPP(m,n)AoyxP(m,n)Aoyx则垂足为轴的垂线作过,,)2(AxP有上任意一点是双曲线设:,)0(),(kxkynmP≠=以上两个性质在课标内没有提及，但在这几年的中考中都有出现，所以在这里要把它总结出来。面积性质（二）函数正比例函数反比例函数解析式图象形状K>0K<0位置增减性位置增减性y=kx(k≠0)(k≠0)y=xk直线双曲线经过一三象限y随x的增大而增大位于一三象限在每个象限内y随x的增大而减小经过二四象限位于二四象限y随x的增大而减小在每个象限内y随x的增大而增大填表分析正比例函数和反比例函数的异同强调：自变量x增大或减小时，反比例函数的两支曲线都无限接近于坐标轴，但是永远不能到达x轴或y轴。几何意义：反比例函数图像的任意一点向X轴和Y轴作垂线，它们与坐标轴围成的矩形面积于。k①②③①②③④⑤⑥④⑤⑥y=3x-1y=3x-1y=2xy=2x22y=y=2x33y=3xy=3xy=y=113x3xy=xx11下列函数中哪些是正比例函数？哪些是反比例函数?1.已知函数反比例喊y=,当x=-1时，则y=__2、已知反比例函数y=图像经过点（-3，4）函数,则k=___。-2-122xkx函数的图象在二、四象限，则m的取值范围是.m-2m-2xxy=y=游戏规则：五个金蛋中任选其中一个金蛋，如果出现金花，大家鼓掌通过，否则你必须回答其中的问题。函数的图象在第象限，在每个象限内，y随x的增大而_____.y=xx55二,四增大双曲线过点(－3,_),(，2)y=y=1212xxm<2P（2，3）Oyx请你根据图象求函数的解析式?挑战挑战““图形信息图形信息””提高从函数的图象中获取信息的能力提高从函数的图象中获取信息的能力xky当你看到下面的图象时当你看到下面的图象时,,你能从中知道些什你能从中知道些什么么??xxyyooxxyyooxkyxxyyooxkybkxy回顾与思回顾与思考考x/x/人人ooooY/Y/吨吨Y/Y/吨吨Y/Y/吨吨Y/Y/吨吨x/x/人人x/x/人人x/x/人人(A)(B)(C)(D)(A)(B)(C)(D)xayC1.1.某村的粮食总产量为某村的粮食总产量为((为常数为常数),),设该村粮食设该村粮食的人均产量为的人均产量为((吨吨),),人口数为人口数为((人人),),则与之间的则与之间的函数函数图象大致是图象大致是().().aayyxx2.2.已知圆柱的侧面积是已知圆柱的侧面积是,,若圆柱底面半径为若圆柱底面半径为,,高为高为,,则与的函数图象大致是则与的函数图象大致是().().210cmrcmhcmhro(A)(B)(C)(D)r/cmh/cmor/cmh/cmor/cmh/cmor/cmh/cmC关注生活（（11）若点）若点A(A(77,y,y11),B(),B(55,y,y22))，则，则yy11,y,y22的大小关的大小关系是系是::。。若点若点AA、、BB都在反比例函数的图象上都在反比例函数的图象上xy2（（22）若点）若点A(A(77,y,y11),B(),B(-5-5,y,y22))，则，则yy11,y,y22的大小关的大小关系是系是::。。利用图像法或代入法。增减性，一定要考虑在每一象限内。同一象限按增减，跨越象限怎么办？反比例函数的图象上有点A（1，6），分别做A点的坐标轴垂线，试求垂线与坐标轴围成的矩形的面积。x6y变式一：反比例函数的图象上有点B（2，3），分别做B点的坐标轴垂线，试求垂线与坐标轴围成的矩形的面积。变式二：反比例函数的图象上有点C（－3，－2），分别做C点的坐标轴垂线，试求垂线与坐标轴围成的矩形的面积。猜测：对于任意一个在函数上的点P，它与两坐标轴的垂线与坐标轴围成的矩形的面积有什么规律？推广：对于任意一个在函数上的点P，它与两坐标轴的垂线、原点的连线以及坐标轴围成的三角形的面积有什么规律？永远不变的就是“变”永远不变的就是“变”S...