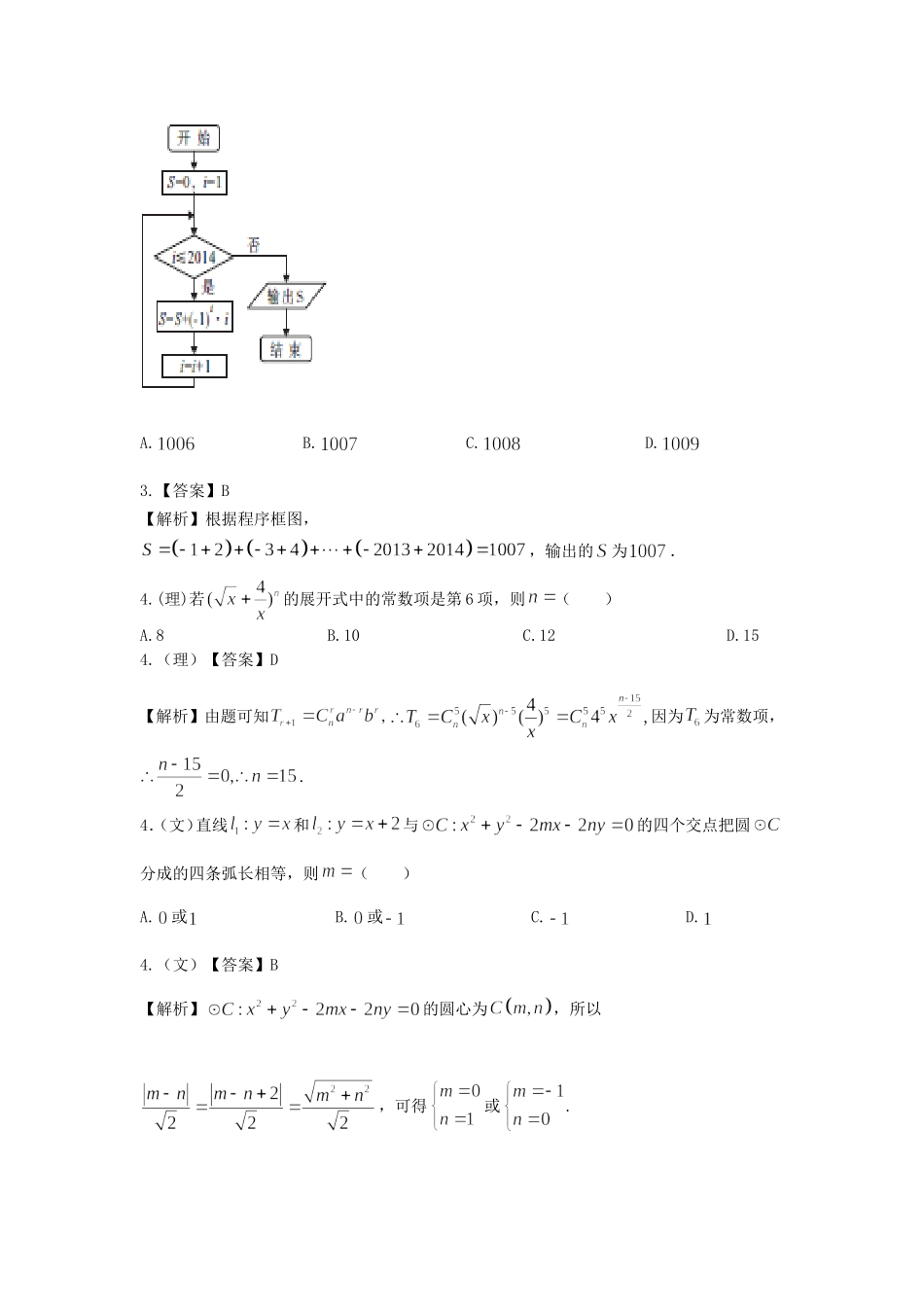
2014届先知新课标数学模拟卷150分,120分钟第I卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.)1.(理)已知集合,,则()A.B.C.D.1.(理)【答案】C【解析】,故.1.(文)设全集,,则()A.B.C.D.1.(文)【答案】C【解析】.2.()A.B.C.D.2.【答案】D【解析】故选D.3.执行如图所示的程序框图,输出结果()A.B.C.D.3.【答案】B【解析】根据程序框图,,输出的为.4.(理)若的展开式中的常数项是第6项,则()A.8B.10C.12D.154.(理)【答案】D【解析】由题可知因为为常数项,.4.(文)直线和与的四个交点把圆分成的四条弧长相等,则()A.或B.或C.D.4.(文)【答案】B【解析】的圆心为,所以,可得或.5.若点是不等式组表示的可行域内的任意一点,则点到直线的距离的最小值是()A.B.C.D.5.【答案】C【解析】如图画出可行域是如图所示的的边界及内部,容易看出当点移动到处时,到直线的距离最小,最小值为6.以表示等差数列的前项和,若,则下列不等关系不一定成立的()A.B.C.D.6.【答案】D【解析】因为,所以,由是等差数列,可得,故,A一定成立;因为,所以,B一定成立;,所以,C一定成立;,所以符号不确定,所以D不一定成立,答案为D.7.“”是“函数在区间内单调递减”的()A.充分不必要条件B.必要不充分条件C.充分必要条条件D.既不充分也不必要条件7.【答案】C230xy230xyxyOABC【解析】在上单调递减等价于在区间无实根,即或,也就是,故是函数在上单调递减的充要条件.8.设是任意的非零向量,且相互不共线,则①;②;③若存在唯一实数组,使,则共面;④中,是真命题的个数是()A.0B.1C.2D.38.【答案】B【解析】由向量数量积运算不满足结合律可知①错误;由向量的加减法三角形法则可知,当非零且不共线时,,故②正确;当时,成立,但不共面,故③错误;因为,故④错误.答案为B.9.(理)设,下列关系式成立的是()A.B.C.D.9.(理)【答案】C【解析】,,所以,又,所以,,所以,故A,B错误;,故C正确;.9.(文)函数的图象如图所示,若函数与轴有两个不同交点,则的取值范围是()A.B.C.D.9.(文)【答案】D【解析】函数与轴有两个不同交点,即方程有两个不同的解,由知,与有两个不同的交点,结合图形可知.故选D.10.如图,边长为的等边的中线与中位线交于点,已知是绕旋转过程中的一个图形,对于下列叙述错误的是()A.平面平面B.∥平面C.三棱锥的体积最大值为D.直线与直线可能共面10.【答案】D【解析】A中由已知可得四边形是菱形,则,所以平面,所以面面,A正确;又∥,∴∥平面;B正确;当面⊥面时,三棱锥的体积达到最大,最大值为,C正确;在旋转过程中与直线始终异面,D不正确.11.(理)在区域内随机取一个点,则此点到点的距离大于的概率是()xyODAA.B.C.D.11.(理)【答案】D【解析】如图,因为点在圆上,所以到点的距离大于的构成的区域是区域内去除它与区域公共部分剩下的部分,剩下部分面积为,故所求事件的概率为.11.(文)椭圆:与双曲线:有公共焦点,曲线,在第一象限交于点,的中点分别为,为坐标原点,四边的周长为则的周长是()A.B.C.D.11.(文)【答案】C【解析】因为的中点分别为,是的中点,所以四边形为平行四边形,故其周长为,可得又因为椭圆与双曲线共焦点,所以,可得,的周长为.12.(理)如图内外两个椭圆的离心率相同,从外层椭圆顶点向内层椭圆引切线.设内层椭圆方程为,则外层椭圆方程可设为.第12题图若与的斜率之积为,则椭圆的离心率为()A.B.C.D.12.(理)【答案】C【解析】设切线的方程为,则由,同理,所以,故.选C.12.(文)同理科11题第II卷(非选择题共90分)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置)13.(理)已知直线与曲线切于点,则的值为.13.(理)【答案】3【解析】由条件知在直线上,∴,又在曲线上,∴, ,∴,∴.13.(文)函数的定义域为.13.(文)【答案】【解析】.14.设的内角所对边的长分别为,若,,则角.14.【答案】【解析】由可得,又,所以可令,可得,故.15.某几何体的三视图如图所示,则...