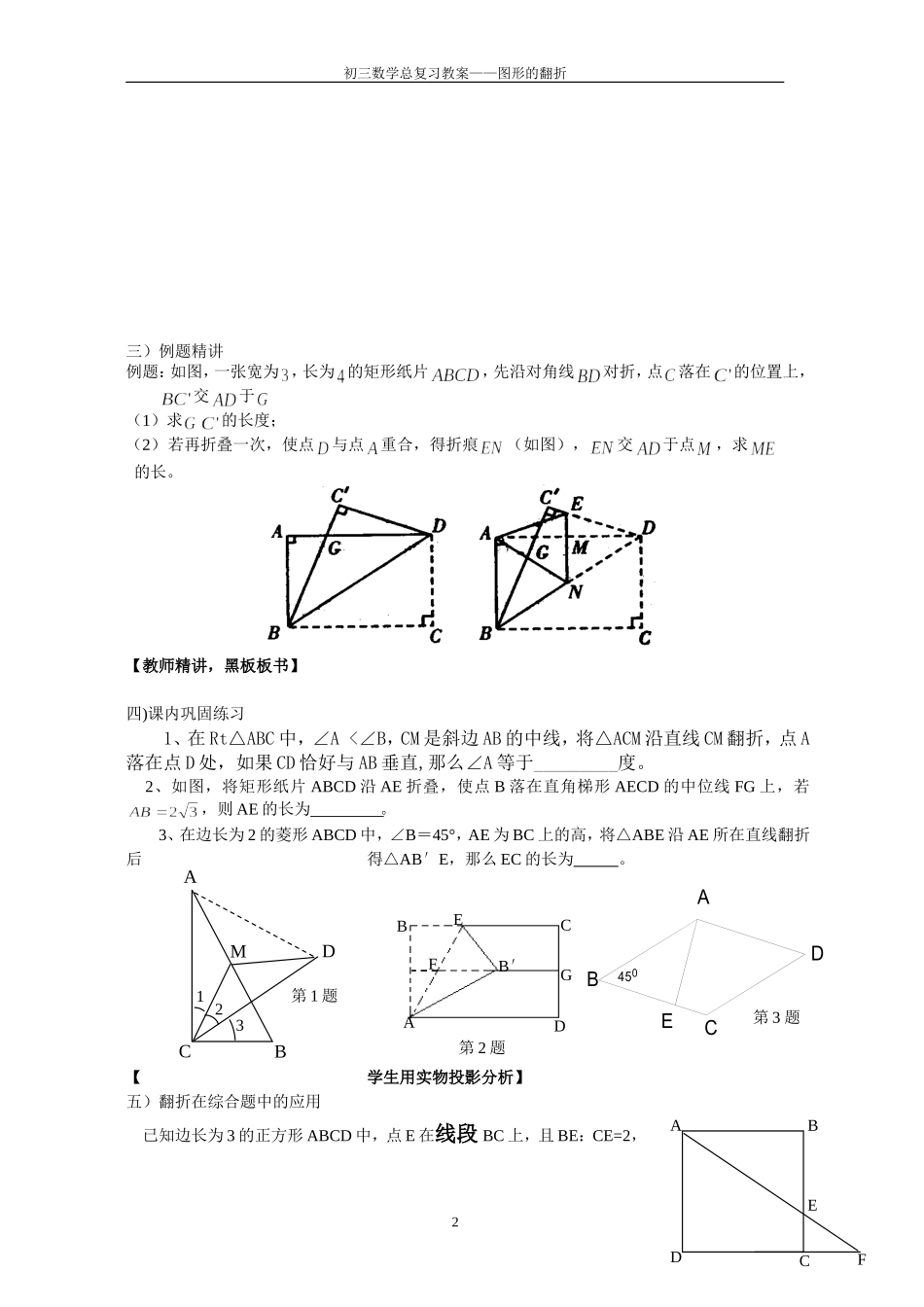
MCBADECBA图一MCBA图二初三数学总复习教案——图形的翻折【教学设计】初三数学总复习——图形的翻折上海市风华初级中学程慧一、教学目标:1、理解图形翻折的直观意义;2、认识平面图形翻折的过程,在实例中理解轴对称的意义;根据要求能画出翻折后的图形;3、知道翻折后图形的形状、大小保持不变;二、教学重点与难点:教学重点:理解图形翻折的意义及相关性质,会画经过翻折后的图形教学难点:利用图形翻折后的性质解决综合问题。三、教学方法和手段:主要采用讨论式和启发式教学方法,利用多媒体辅助教学。四、教学过程一)复习引入如图一,画出△ABC沿着直线DE翻折后的图形。如图二,△ABC沿着某条直线翻折后,点A落在点M处,请画出折痕及翻折后的图形。【黑板演示,理清依线翻折与依点翻折的不同作图方法;引导学生归纳翻折后图形的性质】翻折后图形的性质:1、翻折后得到的图形与原图形形状相同、大小不变,并且对应角、对应线段相等2、折痕所在的直线即为翻折前后两个图形的对称轴3、翻折后,图形对应点的连线段被对称轴垂直且平分二)画一画1、如图1已知:在Rt△ABC中,CM是斜边AB的中线,将△ACM沿直线CM翻折,点A落在点D处,画出翻折后的图形。2、如图2已知:RtABC△中,CM是斜边AB的中线,将△ABC沿某直线折叠,使点C落在M上,折痕与AC的交点为E,与直线BC的交点为F,连接EM,CF。画出翻折后的图形。【关键是找出对称点,利用对称性画出翻折后的图形;学生画,教师用多媒体演示,进行点评总结】1CBAMEF图2ADCFEBBECAB′GDFACBDM123初三数学总复习教案——图形的翻折三)例题精讲例题:如图,一张宽为,长为的矩形纸片,先沿对角线对折,点落在的位置上,交于(1)求的长度;(2)若再折叠一次,使点与点重合,得折痕(如图),交于点,求的长。【教师精讲,黑板板书】四)课内巩固练习1、在Rt△ABC中,∠A<∠B,CM是斜边AB的中线,将△ACM沿直线CM翻折,点A落在点D处,如果CD恰好与AB垂直,那么∠A等于_________度。2、如图,将矩形纸片ABCD沿AE折叠,使点B落在直角梯形AECD的中位线FG上,若,则AE的长为。3、在边长为2的菱形ABCD中,∠B=45°,AE为BC上的高,将△ABE沿AE所在直线翻折后得△AB′E,那么EC的长为。【学生用实物投影分析】五)翻折在综合题中的应用已知边长为3的正方形ABCD中,点E在线段BC上,且BE:CE=2,2450EDCAB第3题第2题第1题DFENB'CBA初三数学总复习教案——图形的翻折连结AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点处.(1)如图:若点E在线段BC上,求CF的长;【引导学生运用基本图形快速解出CF=1.5】(2)求sin∠DAB1的值;【画出如图1翻折后的图形,利用勾股定理解得==】(3)题设中点E在射线BC上时,求sin∠DAB1的值【画出翻折后的图形,利用勾股定理解得==。体现分类讨论思想】(4)如果题设中“BE:CE=2”改为“BE:CE=X”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积与的关系式及定义域.(只要写出结论,不要解题过程)【若点E在线段BC上,,定义域为;若点E在边BC的延长线上,,定义域为.】六)小结1、解决翻折这类题抓住翻折前后两个图形是全等的,弄清翻折后不变的要素。会画出翻折后的图形;2、利用图形翻折的特征和性质解决数学问题;3、结合中考命题热点和热点趋势,带领学生熟悉中考题型。七)作业布置“初三数学总复习——图形的翻折”教学设计说明3图1ADCFEBBM12初三数学总复习教案——图形的翻折图形翻折是初中数学中常见的图形运动之一。根据《初三数学学科基本要求》一书,要求初三的学生能理解图形翻折的直观意义、认识平面图形翻折的过程、在实例中理解轴对称的意义;根据要求能画出依点翻折和依线翻折后的图形;知道翻折后图形的形状、大小保持不变;能运用翻折后图形的性质解决数学问题,提高学生解综合问题的能力。为达到以上教学目的,设计以下几个教学环节:1、复习引入教师黑板直观演示图形依线翻折和依点翻折的作图方法,从而“唤醒”学生图形翻折的知识,在师生互动中完成作图,归纳出图形翻折的两种类型和主要性质;并设计“画一画”的环节,学生自己动手画出翻折后的图形,为后面的解题设下...