第十二章 结构的极限荷载VIP免费

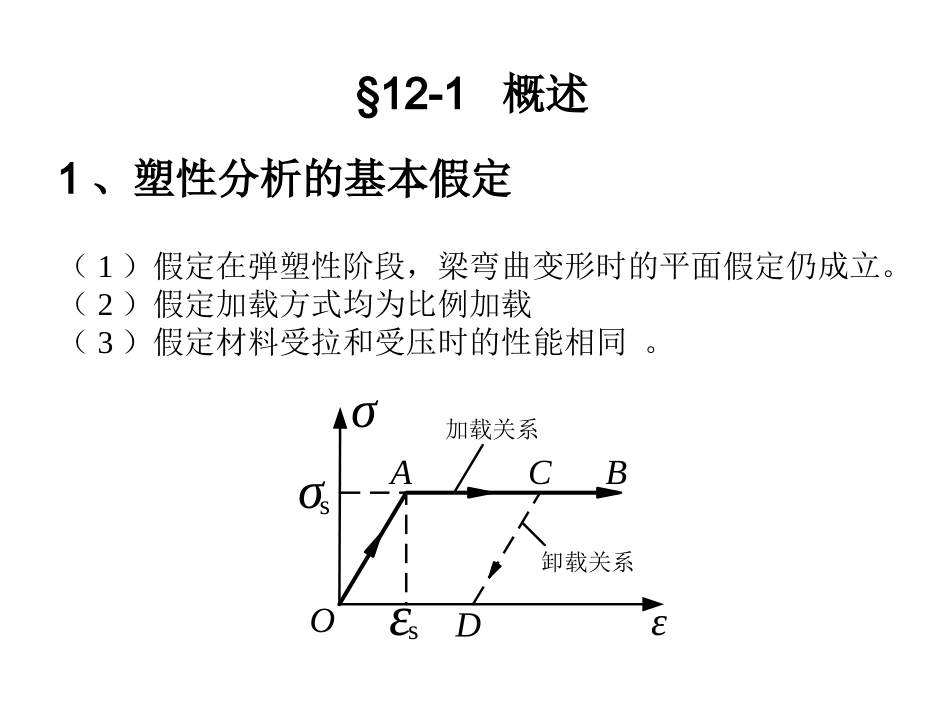
结构力学结构力学STRUCTURALMECHANICSSTRUCTURALMECHANICSChap12结构的稳定计算12-1概述12-2超静定梁的极限荷载12-3超静定刚架的极限荷载1、塑性分析的基本假定（1）假定在弹塑性阶段，梁弯曲变形时的平面假定仍成立。（2）假定加载方式均为比例加载（3）假定材料受拉和受压时的性能相同。OABCDεσσεs加载关系卸载关系s§12-1概述2、塑性分析的基本概念hb2b2MMσσσsσsσsσs弹性核σsσs弹性极限弯矩，或称为屈服弯矩截面的极限弯矩塑性铰极限荷载下图所示为等截面T形简支梁：截面的极限弯矩值us11s22s12()MAaAaSSFPl/2l/2a2a1A2A1形心轴等分面积轴形心σσsσsσsσsσs对称轴下面以上图所示的等截面T形简支梁为例，说明极限荷载的确定方法。FpuABC塑性铰l/2l/2M图uM极限荷载为uPu4MFl§11-2超静定梁的极限荷载静定梁无多余约束，只要有一个截面出现塑性铰就变成了机构而丧失承载能力。qq原结构破坏机构超静定结构由于存在多余约束，因此要形成足够多的塑性铰才变成机构而丧失承载能力以致破坏。FPFP原结构破坏结构FPFPMu原结构破坏机构FPFPMu原结构破坏机构1、单跨超静定梁的极限荷载如图（a）所示的等截面单跨超静定梁，在加载的初始过程，梁处于弹性阶段。弯矩图如图（b）所示，截面A的弯矩最大。当荷载超过Fps后，A端弯矩首先达到极限弯矩Mu并形成塑性铰。当荷载继续增大，C截面也达到极限弯矩Mu。此时，由于两个塑性铰的存在，超静定梁转化为静定梁。此后再继续加载，A、C截面弯矩Mu保持不变，两个塑性铰继续存在，而截面B的弯矩则继续增大。当截面B的弯矩也达到Mu形成塑性铰时，梁即变为破坏机构（图（c））。此时，荷载达到极限值Fpu，相应的弯矩图如图（d）所示。FPabBClA2P2Fabl2P2FbalP2FablFPuABCAθBACθθθBθCPuFabluMuMuM(a)(b)(c)(d)2、能量法上图（c）中，设机构沿荷载正方向发生任意微小的虚位移，根据虚功原理，外力虚功等于变形虚功，可得Puuuuu2CABCABFMMMM由于CAaCBb故求得极限荷载如下：Puu2lFMab例12-1由以上计算可看出，确定超静定梁的极限荷载不需考虑结构弹塑性变形的发展过程，只需确定塑性铰的位置，就可由静力平衡条件或虚功原理直接求出。根据单跨超静定梁弯矩图的特点可知，其塑性铰应满足下述两条规则：①塑性铰只能出现在固定端、集中荷载作用点或均布荷载段剪力为零处；②当作用在梁上所有的荷载均向下时，负塑性铰只能出现在固定端处，跨中不可能出现负塑性铰。例12-22、多跨连续梁的极限荷载设多跨连续梁在每一跨度内为等截面，但各跨的截面可以彼此不同。若荷载按比例增加，且方向向下作用在梁上。由于每跨内的最大负弯矩只可能在跨度两端出现，因此相应的负塑性铰也只可能在两端出现，故破坏机构只能在各跨内独立形成。FP1u1Mu2MFP2ABDECABDECABDECABDEC例12-3例12-4§12-3超静定刚架的极限荷载利用穷举法计算刚架的极限荷载，首先需要确定刚架破坏机构的所有可能形式，然后一一计算每一种破坏机构所对应的可破坏荷载，选取其中的最小值即为极限荷载。确定刚架的破坏机构相对于连续梁而言要复杂一些，通常先确定一些基本破坏机构，简称基本机构。常见的基本机构有梁机构、结点机构、侧移机构、山墙机构，如下图（a）、（b）、（c）、（d）所示。将上述基本机构适当组合，可以得到若干新的破坏机构，称为组合机构或联合机构。(a)(b)(c)(d)在一般情况下，n次超静定结构出现n+1个塑性铰后，即形成破坏机构。对于任一给定刚架，基本机构数m可由它的超静定次数n和可能出现的塑性铰总数h确定，即nhm下图（a）所示刚架，在集中荷载作用下，由弯矩图的形状可知，塑性铰只可能在A、B、C三个截面处出现。刚架的超静定次数为n=1，可能形成的塑性铰个数h=3，基本机构数为213nhm可能的机构为梁机构（图(b)），侧移机构（图(c)）及两机构组成的组合机构（图(d)）。AFP2FPuMuMBCDlllFP2FPθθ2FP2FPθlθFP2FPθθ2lθ(a)(b)(c)(d)对于梁机构，列出虚功方程为Puuu2FlMMuPu3MFl对于侧移机构，列出虚功方程为Puuu2FlMMuPuMFl对于组合机构，列出虚功方程为PuPuuu22FlFlMMuPuMFl因此由上述各FPu值中选取最小者为结构的极限荷载uPuMFl例12-5课件制作中参考了部分网络资源，向原作者致谢！