第7章 机械的运转及其速度波动的调节VIP免费

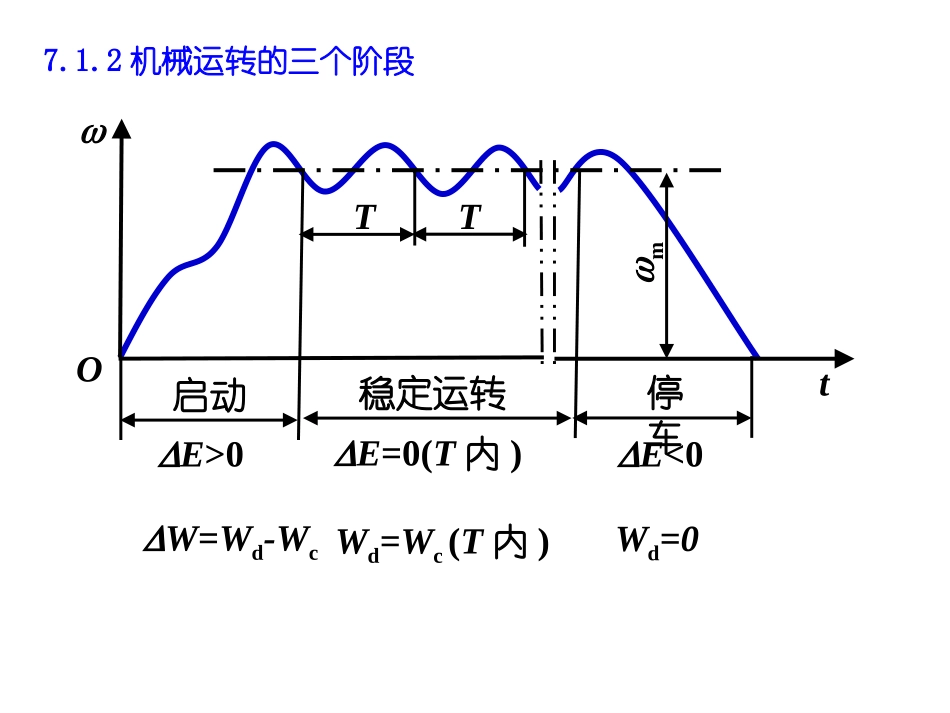
第第77章机械的运转及其速度波动的调节章机械的运转及其速度波动的调节7-1概述7-2机械的运动方程式7-3机械系统的等效动力学模型7-4稳定运转状态下机械的周期性速度波动及其调节7-5机械的非周期性速度波动及其调节本章教学内容7.1概述第3章运动分析,讨论构件间的运动关系（假设原动件作等速运动，忽略了力对机构运动影响）。实际上，机构原动件的运动规律由各构件的质量、转动惯量和作用在机械上的力等因素决定，即原动件的运动规律并非绝对均匀。问题：1）如何确定机械的真实运动规律？2）如何控制机械速度波动的程度？7.1.1研究内容与目的启动稳定运转停车mtOTTE>0E=0(T内)E<0W=Wd-WcWd=Wc(T内)Wd=07.1.2机械运转的三个阶段7.1.2作用在机械上的力当忽略机械中各构件的重力以及运动副中的摩擦力时，作用在机械上的力可分为工作阻力和驱动力两大类：工作阻力驱动力原动机的机械特性：指原动机发出的驱动力与运动参数之间的关系。（1）驱动力为常量（2）驱动力是位移的函数（3）驱动力是速度的函数7.27.2机械的运动方程式机械的运动方程式7.2.1机械运动方程的一般表达式机械的运动方程式——作用在机械上的力、构件的质量、转动惯量和其运动参数之间的函数关系。为了研究问题的方便，对于单自由度的机械系统比较简单的方法就是利用动能定理建立其运动方程式。dE=dW（Pdt）dt瞬间内系统总动能的增量=系统各外力作的元功之和232221231222(/2/2/2/2)SSdEdJmJm1133()dWMFdtPdt系统的运动方程式为：222212231223(/2/2/2/2)SSdEdJmJm1133()MFdt【例7-1】已知曲柄1作为原动件，其角速度为ω1。曲柄1的质心S1在O点，其转动惯量为J1，连杆2的角速度为ω2，质量为m2，其对质心S2的转动惯量为JS2，质心S2的速度为VS2，滑块3的质量为m3，其质心S3在B点，速度为V3。试建立此机构的运动方程的一般表达式。该机构驱动力矩M1和工作阻力F3在瞬间所作的元功为：123s2CB111M)S(A13F【解】该机构瞬间的动能增量为：如果机械系统是由n个活动构件组成的机构若作用于构件i上的作用力为Fi，力矩为Mi，力Fi作用点的速度为vi，构件的角速度为ωi。运动方程的一般表达式为：2211[(/2/2)][(cos)]nniSiSiiiiiiiiidmJFMdt机械运动方程式通式：7.2.2机械系统的等效动力学模型123s2CB111M)S(A13F222212231223(/2/2/2/2)SSdJmJm1133()MFdt2222231212231112SSdJmJm31131()MFdt2222321223e111=SSJJmJm令：3131eMMFdtMJdee121)(21等效动力学模型等效构件Je为等效转动惯量Me为等效力矩假想地具有所有运动构件的动能和所有外力（外力矩）所做功的构件所形成的Ⅰ级机构，称为该机械系统的等效动力学模型。11MeJe123s2CB111M)S(A13F222212231223(/2/2/2/2)SSdJmJm1133()MFdt222232121223333()2SSdJmJm13133()MFdt2222121223e333=SSmJmJm令：1133eFMF23312eedmFdt等效动力学模型等效构件Fe为等效力me为等效质量3Fes3me关于等效构件：是系统中的一个构件；具有真实角速度(速度)；具有假想的Je（me）；作用有假想的Me(Fe)；具有与真实系统相同的动能和外力功。只求单自由度系统的一个构件的真实规律。11Me1Fes1meJe等效转动惯量、等效质量的特征：（1）等效转动惯量Je、等效质量me与运动速度有关，它们是机构位置的函数；（5）mi、Ji各自对应着mei、Jei，并且式子me=∑mei、Je=∑Jei成立；（2）等效转动惯量Je、等效质量me仅仅与速比有关，所以不必求出速度的真实值而可以任选比例尺绘制速度多边形进行Je、me的求解；（4）等效转动惯量Je、等效质量me是假想的转动惯量和质量，不是机械中所有运...