电感和电容的串联电路VIP免费

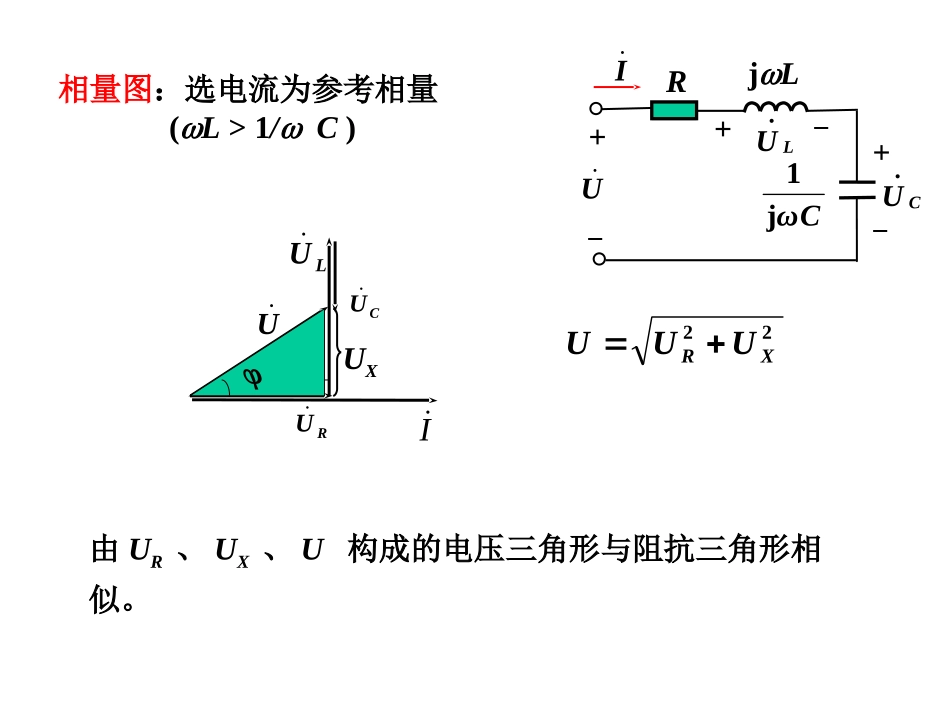
LCRuuLuCi+-+-+-IjLR+-+-+-ULU.CU.Cωj1一、电阻、电感和电容的串联电路由KVLICILIRUUUUCLR1jjICLR)1jj(IXXRCL)]j([IXR)j(9.4阻抗与导纳9.4阻抗与导纳||jZXRIUZ令Z—复阻抗(compleximpedance)；R—电阻(阻抗的实部)；X—电抗(reactance)(阻抗的虚部)；|Z|—复阻抗的模；—阻抗角(impedanceangle)。关系arctg||22RXφXRZ或R=|Z|cosX=|Z|sin|Z|RX<0|Z|RX>0阻抗三角形(impedancetriangle)相量图：选电流为参考相量(L>1/C)由UR、UX、U构成的电压三角形与阻抗三角形相似。LUCUIRUUX22XRUUUIjLR+-+-+-ULU.CU.Cωj1UL>1/C，>0，电路为感性。L<1/C，<0，电路为容性。L=1/C，=0，电路为电阻性IUIUIUR、L、C串联电路的性质Z=R+j(L-1/C)=|Z|∠IjLR+-+-+-ULU.CU.Cωj1|Z|=U/I=u-i例LCRuuLuCi+-+-+-已知：R=15,L=0.3mH,C=0.2F,Hz103,V)60sin(254ftu求i,uR,uL,uC。解其相量模型为IjLR+-+-+-ULU.CU.Cj1V605UΩ4.6354.335.26j5.56j151jjoCωLωRZ5.56j103.0103π2jj34L5.26j102.0103π21j1j64CA4.3149.04.6354.33605ZUI则A)4.3(sin2149.0tiUL=8.42V>U=5V，分电压大于总电压，为什么？ULUCUIRU-3.4°相量图V4.3235.24.3149.015IRURV4.8642.84.3149.0905.56jILULV4.9395.34.3149.0905.261jICUCV)4.3sin(2235.2tuRV)6.86sin(242.8tuLV)4.93sin(295.3tuC二、电阻、电感和电容并联的电路由KCLUCULUGIIIICLRj1jiLCRuiLiC+-iLIjLULICICωj1R+-RIUCLG)j1j(UBBGCL)]j([UBG)j('||jYBGψψUIψUIUIYuiui令Y—复导纳(complexadmittance)；G—电导(导纳的实部)；B—电纳(suspectance)(导纳的虚部)；|Y|—复导纳的模；—导纳角(admittanceangle)。关系arctg||22GB'BGY或G=|Y|cos'B=|Y|sin'导纳三角形(admittancetriangle)|Y|GB>0|Y|GB<02222)(CLGBGIIIIIIY=G+j(C-1/L)=|Y|∠C=1/L，B=0，=0，电路为电阻性，i与u同相。C>1/L，B>0，'>0，电路为容性，i领先u；C<1/L，B<0，'<0，电路为感性，i落后u；R、L、C并联电路的性质相量图：选电压为参考向量(C<1/L，<0)ULI.IGI.'CI.IjLULICICωj1R+-GI|Y|=I/U=i-u三、复阻抗Z正弦激励下，对于无独立源线性网络，可定义入端等效复阻抗纯电阻Z=R纯电感Z=jL=jXL纯电容Z=1/jC=jXCIZU+-无源线性IU+-)(j||defiuXRZIUZ)(j||defiuXRZIUZ四、复导纳Y)'('||jdefuiYBGUIY)'('||jdefuiYBGUIY|Z|RX阻抗三角形|Y|GB导纳三角形对于上述的无独立源线性网络，同样可定义入端等效复导纳：CCLLRBCYBLYRYjj:jj1:/1:纯电容纯电感纯电阻IYU+-无源线性IU+-ZY1五、复阻抗和复导纳等效关系'||j||jφYBGYφZXRZ一般情况G1/RB1/X。若Z为感性，X>0，则B<0，即仍为感性。ZRjXGjBYφφZYXRXBXRRG',||1||,2222BGXRXRXRZYjjj1122同样，若由Y变为Z，则有：XRBGBGBGYZφZXRZφYBGYjjj11||j,'||j22',||1||,2222φφZYBGBXBGGRGjBYZRjX六、阻抗串联、并联的电路两个阻抗串联21ZZZ等效阻抗ZZ1Z2+++---U1U2UI两个阻抗并联2121212111ZZZZZZYYY等效导纳IY+-UZ1Z21I2IUZZZUUZZZU21222111,...