模式识别第2讲VIP免费

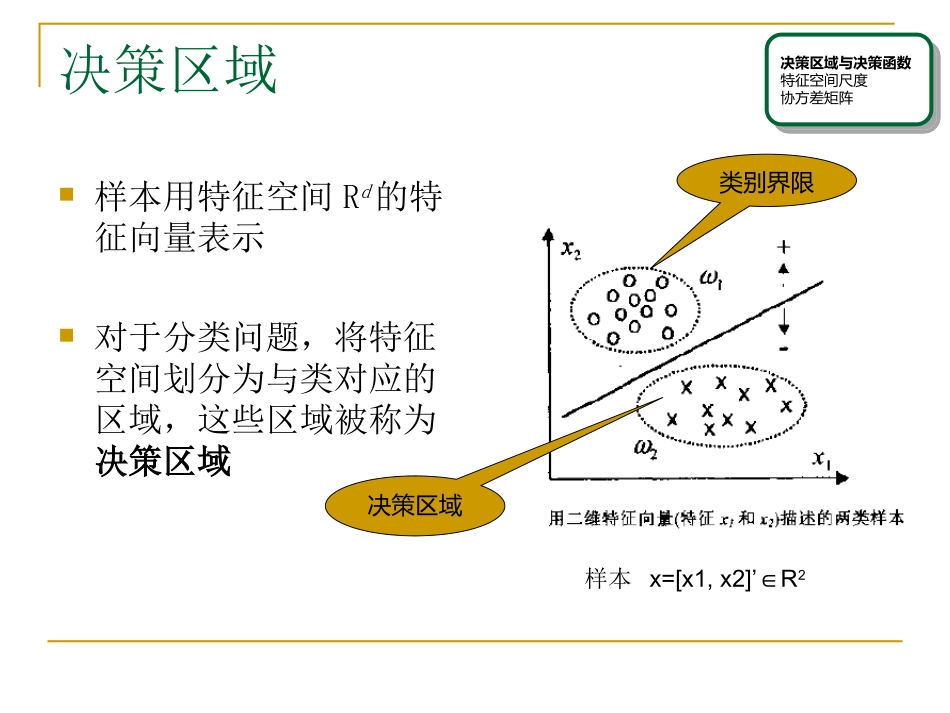
模式识别模式识别——原理、方法及应用第2次课程概要模式判别决策区域和决策函数广义决策函数分类超平面特征空间尺度协方差矩阵决策区域样本用特征空间Rd的特征向量表示对于分类问题，将特征空间划分为与类对应的区域，这些区域被称为决策区域决策区域类别界限样本x=[x1,x2]’R∈2决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵决策函数**'')(0XWwXWxd0)(02211wxwxwxd0...)(011wxwxwxddd决策函数样本x=[x1,x2]’R∈2决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵决策函数决策函数样本x=[x1,x2]’R∈2决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵增广特征向量权向量**'')(0XWwXWxd]...1[*]...[*]...[1101dddxxXwwwWwwW增广权向量决策函数超平面的两个参数任意一点z到超平面的距离决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵：决策面或判别式d维线性平面超平面)(xd确定超平面的两个参数如下WWnWwD,00线性决策函数遇到什么情况没法有效分类？广义决策函数ij,,)(,)(并且如果如果jjiixxdxxd决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵只要各类别间没有重叠，我们总能在Rd空间中找到一个广义决策函数，将第i类从全体类别中分离出来。广义决策函数例1：应用二次决策函数的一个两类判别问题决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵2)(xxd)ln()(2xxd49广义决策函数例2：广义决策函数为函数的线性组合的一个两类判别问题决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵)]'()...(1[***')(...)()(1011xfxfyywwxfwxfwxdkkk25.0]y1[]'125.0[)(yyg变换25.0)1()1()(2221xxxd广义决策函数例3：广义决策函数为多项式的一个两类判别问题决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵0211221322421522162217328319321102311122211242134114)(wxwxwxxwxwxwxxwxxwxwxwxxwxxwxxwxwxwxd两个特征，15个权重系数十四个特征，1个偏差量多项式决策函数的计算量决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵d维特征空间的模式识别问题，为了得到一个k次的多项式决策函数需要计算!!)!(),(kdkdkkdC个多项式系数如何解决多分类问题第一种情况：绝对可分任何一个类可以从其他所有的类中分离出来决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵可通过推广两类分类问题，即采用多阶段二分类方法解决多类问题。ij,,)(,)(并且如果如果jjiixxdxxd},..1,,0)(,0)(;{ijcjixdxdxRjii决策函数决策域决策函数决策域如何解决多分类问题第二种情况：成对可分不能达到绝对可分，但可以成对线性可分jijiijxxdxxd,0)(,0)(决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵},..1,,0)(;{ijcjixdxRiji决策函数决策域常用范数能够度量特征向量之间距离的四种常用方法决策区域与决策函数特征空间尺度协方差矩阵决策区域与决策函数特征空间尺度协方差矩阵|)(|maxiiiCmxmxdiiicmxmx1||diiismxmx12)(diiiemxmx12)(切比雪夫范数棋盘格范数欧几里得范数欧几里得平方范数diiiemxmx12)(乘方范数rdipiirpmxmx/11/)(p是控制各维度差异的权重，r则控制样本逐渐分开的时候，它们之间距离的增长速度。r=p，明可夫斯基范数。r=p=2，欧几里得范数。r=p=1，棋盘格范数。r=p∞，切比雪夫范数。|)(|maxiiiCmxmxdiiicmxmx1||diiismxmx12)(diiiemxmx12)(决策区域与决策函数特...