极限的四则运算法则VIP免费

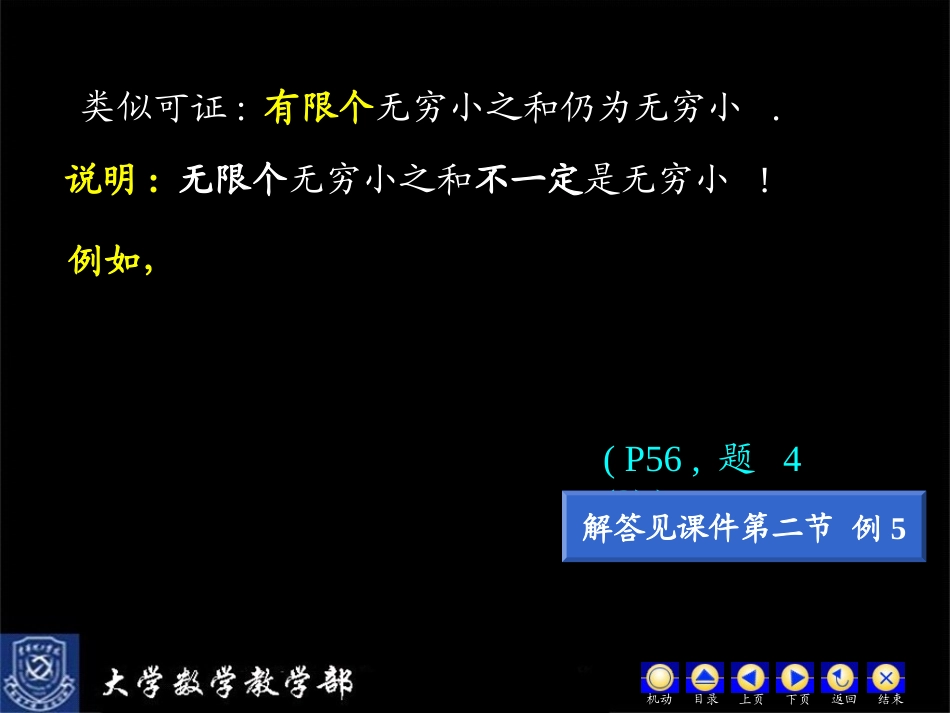
第一章二、极限的四则运算法则三、复合函数的极限运算法则一、无穷小运算法则第五节机动目录上页下页返回结束极限运算法则时,有,,min21一、无穷小运算法则定理1.有限个无穷小的和还是无穷小.证:考虑两个无穷小的和.设,0当时,有当时,有取则当00xx22因此这说明当时,为无穷小量.机动目录上页下页返回结束说明:无限个无穷小之和不一定是无穷小!例如，nnnnnn2221211lim1(P56,题4(2))解答见课件第二节例5机动目录上页下页返回结束类似可证:有限个无穷小之和仍为无穷小.定理2.有界函数与无穷小的乘积是无穷小.证:设Mu又设,0lim0xx即,0当时,有M取,,min21则当),(0xx时,就有uuMM故即是时的无穷小.推论1.常数与无穷小的乘积是无穷小.推论2.有限个无穷小的乘积是无穷小.机动目录上页下页返回结束例1.求解:01limxx利用定理2可知xxysin说明:y=0是的渐近线.机动目录上页下页返回结束二、极限的四则运算法则,)(lim,)(limBxgAxf则有证:因,)(lim,)(limBxgAxf则有BxgAxf)(,)((其中,为无穷小)于是)()()()(BAxgxf)()(BA由定理1可知也是无穷小,再利用极限与无穷小的关系定理,知定理结论成立.定理3.若机动目录上页下页返回结束推论:若,)(lim,)(limBxgAxf且),()(xgxf则.BA(P45定理5))()()(xgxfx利用保号性定理证明.说明:定理3可推广到有限个函数相加、减的情形.提示:令机动目录上页下页返回结束定理4.若,)(lim,)(limBxgAxf则有提示:利用极限与无穷小关系定理及本节定理2证明.说明:定理4可推广到有限个函数相乘的情形.推论1.)(lim)](lim[xfCxfC(C为常数)推论2.nnxfxf])(lim[)](lim[(n为正整数)例2.设n次多项式试证).()(lim00xPxPnnxx证:)(lim0xPnxx机动目录上页下页返回结束为无穷小(详见P44)B2B1)(1xg)(0xx定理5.若,)(lim,)(limBxgAxf且B≠0,则有证:因,)(lim,)(limBxgAxf有,)(,)(BxgAxf其中,设BABA)(1BB)(AB无穷小有界因此由极限与无穷小关系定理,得BAxgxf)()(为无穷小,机动目录上页下页返回结束定理6.若,lim,limByAxnnnn则有)(lim)1(nnnyxnnnyxlim)2(,00)3(时且当BynBAyxnnnlimBABA提示:因为数列是一种特殊的函数,故此定理可由定理3,4,5直接得出结论.机动目录上页下页返回结束x=3时分母为0!31lim3xxx例3.设有分式函数其中都是多项式,试证:证:)(lim0xRxx)(lim)(lim00xQxPxxxx说明:若不能直接用商的运算法则.例4.)3)(3()1)(3(lim3xxxxx若机动目录上页下页返回结束例5.求解:x=1时3245lim21xxxx031241512分母=0,分子≠0,但因机动目录上页下页返回结束例6.求解:时,分子22111125934limxxxxx分子分母同除以,2x则分母“抓大头”原式机动目录上页下页返回结束一般有如下结果：为非负常数)(如P47例5)(如P47例6)(如P47例7)mmmxaxaxa110limnnnbxbxb110机动目录上页下页返回结束三、复合函数的极限运算法则定理7.设且x满足时,,)(ax又则有证:,0,0当au0时,有Auf)(,02当200xx时,有ax)(对上述取,,min21则当00xx时ax)(au故0Auf)(,①因此①式成立.机动目录上页下页返回结束定理7.设且x满足时,,)(ax又则有])([lim0xfxx说明:若定理中,)(lim0xxx则类似可得])([lim0xfxxAufu)(lim机动目录上页下页返回结束例7.求解:令932xxu已知ux3lim61(见P46例3)∴原式=6166(见P33例5)机动目录上页下页返回结束例8.求解:方法1,xu则,1lim1ux令11112uuxx1u∴原式)1(lim1uu2方法21)1)(1(lim1xxxx)1(lim1xx2机动目录上页下页返回结束内容小结1.极限运算法则(1)无穷小运算法则(2)极...