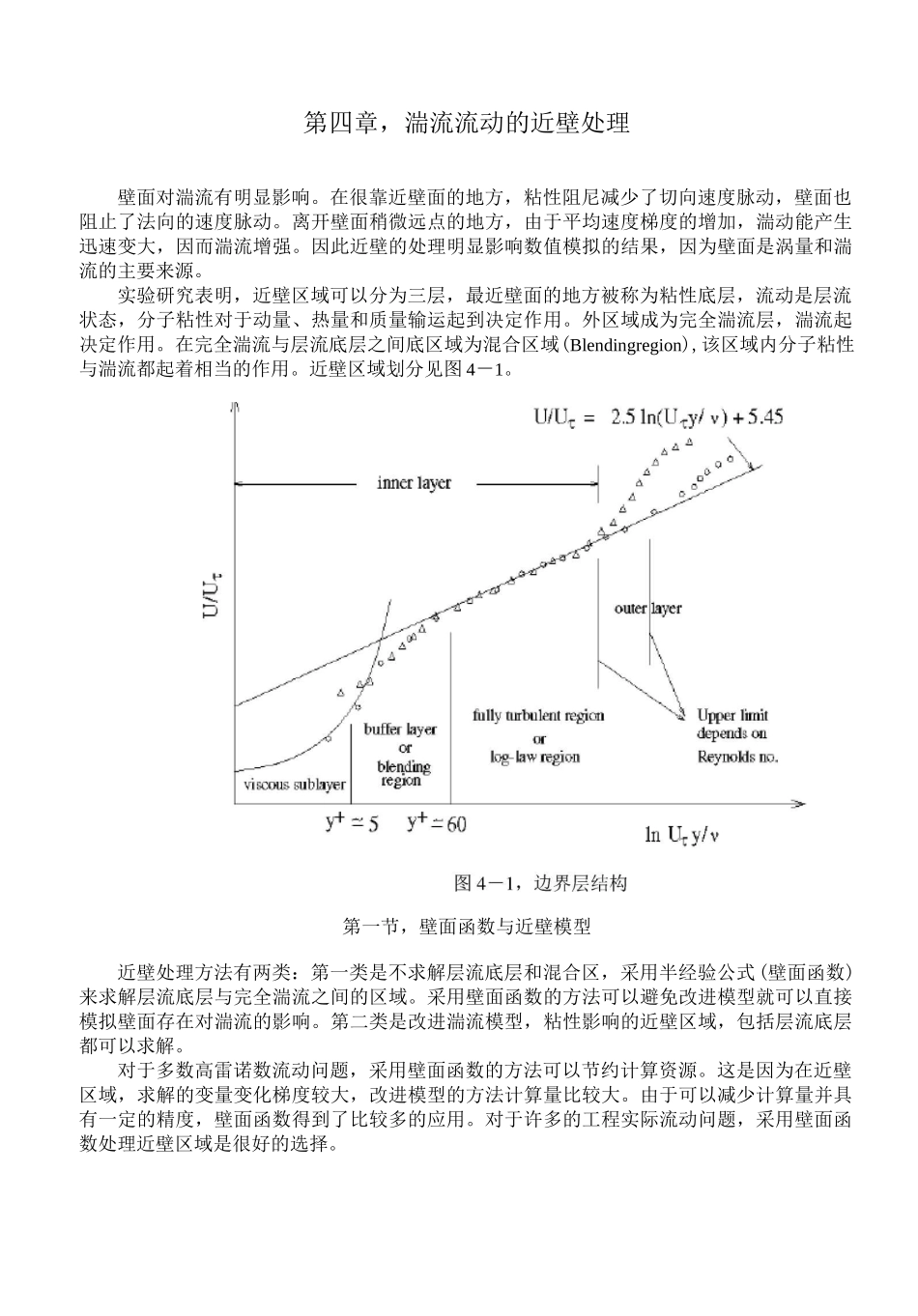
第四章,湍流流动的近壁处理壁面对湍流有明显影响。在很靠近壁面的地方,粘性阻尼减少了切向速度脉动,壁面也阻止了法向的速度脉动。离开壁面稍微远点的地方,由于平均速度梯度的增加,湍动能产生迅速变大,因而湍流增强。因此近壁的处理明显影响数值模拟的结果,因为壁面是涡量和湍流的主要来源。实验研究表明,近壁区域可以分为三层,最近壁面的地方被称为粘性底层,流动是层流状态,分子粘性对于动量、热量和质量输运起到决定作用。外区域成为完全湍流层,湍流起决定作用。在完全湍流与层流底层之间底区域为混合区域(Blendingregion),该区域内分子粘性与湍流都起着相当的作用。近壁区域划分见图4-1。第一节,壁面函数与近壁模型近壁处理方法有两类:第一类是不求解层流底层和混合区,采用半经验公式(壁面函数)来求解层流底层与完全湍流之间的区域。采用壁面函数的方法可以避免改进模型就可以直接模拟壁面存在对湍流的影响。第二类是改进湍流模型,粘性影响的近壁区域,包括层流底层都可以求解。对于多数高雷诺数流动问题,采用壁面函数的方法可以节约计算资源。这是因为在近壁区域,求解的变量变化梯度较大,改进模型的方法计算量比较大。由于可以减少计算量并具有一定的精度,壁面函数得到了比较多的应用。对于许多的工程实际流动问题,采用壁面函数处理近壁区域是很好的选择。如果我们研究的问题是低雷诺数的流动问题,那么采用壁面函数方法处理近壁区域就不合适了,而且壁面函数处理的前提假设条件也不满足。这就需要一个合适的模型,可以一直求解到壁面。FLUENT提供了壁面函数和近壁模型两种方法,以便供用户根据自己的计算问题选择。4.1.1壁面函数FLUENT提供的壁面函数包括:1,标准壁面函数;2,非平衡壁面函数两类。标准壁面函数是采用LaunderandSpalding[L93]的近壁处理方法。该方法在很多工程实际流动中有较好的模拟效果。4.1.1.1标准壁面函数根据平均速度壁面法则,有:U*=-iln(Ey*)4一1kUC1/4k1/2pC1/4k1/2y其中,U*三p»—,y*三―pp,并且T/p卩wk=0.42,是VonKarman常数;E=9.81,是实验常数;U是P点的流体平均速度;k是P点的湍动能;y是P点到壁面的距离;卩是流体的动力粘性系数。"p通常,在y*>30~60区域,平均速度满足对数率分布。在FLUENT程序中,这一条件改变为y*>11.225。当网格出来y*<11.225的区域时候,FLUENT中采用层流应力应变关系,即:U*=y*。这里需要指出的是FLUENT中采用针对平均速度和温度的壁面法则中,采用了y*,而不是y+(三puy/卩)。对于平衡湍流边界层流动问题,这两个量几乎相等。T根据雷诺相似,我们可以根据平均速度的对数分布,同样给出平均温度的类似分布。FLUENT提供的平均温度壁面法则有两种:1,导热占据主要地位的热导子层的线性率分布;2,湍流影响超过导热影响的湍流区域的对数分布。温度边界层中的热导子层厚度与动量边界层中的层流底层厚度通常都不相同,并且随流体介质种类变化而变化。例如,高普朗特数流体(油)的热导子层厚度比其粘性底层厚度小很多;对于低普朗特数的流体(液态金属)相反,热导子层厚度比粘性底层厚度大很多。(T—T)pcC1/4k1/2T*三wpp_MP—4一2q(y*y*)4-是流体定压比热;q壁面热流;T近邻pp是流体密度;Pr=^c/k为分子普朗特数;Pr是湍流普朗特数,壁面取pft1C1/4k1/2Pry*+pPr——U22q"pPr1ln(Ey*)+P+k1C1/4k1/22p〒[PrtUp+(Pr-Prt)Uc2]其中P的计算采用下列公式[L93]P—兀/4sin(兀/4)t其中,k是流体导热系数f壁面控制体温度;T壁面温度;w0.85;A=26,是VanDries常数;k=0.42,是VonKarman常数;E=9.793,是壁面函数常数;U是y*=y*时的平均速度大小。cTFluent中,当选择了流体介质后,就可以根据流体介质的物理性质,计算出分子普朗特数,热导子区厚度y*,存储备用。在求解的时候,根据y*与已经存储的y*之间大小关系,判断是TT采用线性法则还是对数法则来计算壁面温度T或热流率q”。在采用雷诺应力模型或k-s双方程模型时,包括壁面近邻的控制体的湍动能都要计算,其边界条件为湍动能在壁面法向方向上梯度为零。湍动能产生项G及耗散率是湍动能输运方程的源项组成部分,根据局部平衡假设来计算。k...