A、Ia+bI=Ia-bI1B、IaI=IbI=Ia-bIc、IaI=IbI=Ia+bID、Ia+bI=Ia-bI=2IaI、平面向量的几何意义✓平面向量既有坐标表示,也有几何表示(即有向线段表示),利用平面向量的几何意义解题,在解决某些数学问题时往往能起到避繁就简的效果。✓a+bn首尾相连,首指向尾a-bn共起点,指向被减向量Ia+tb1=1a-tbIna丄bIa+bI=Ia-bIn对角线相等的平行四边形,即矩形✓(a+b)(a-b)=0n对角线互相垂直的平行四边形,即菱形二、例题精析—F—■>—*—¥■例1、(2017,崂山区校级期末改编)已知a,b是非零向量,则下列条件中a,b夹角等于12Oo的是()—¥■—F―►—F-―►—►—*■—►【解析】由题知a,b是非零向量,则Ia+bI=Ia-bI表示对角线相等的平行四边形,即为矩形,故a,b夹—F—F―*—■>—F—■>角为900;而IaI=IbI=Ia-bI表示a,b所在的边与其中一条对角线长度相等,故构成的三角形为等边三角—¥—►—F—F―►—►—!»■T形,故a,b夹角为60。;IaI=IbI=Ia+bI表示a,b所在的边与其中一条对角线长度相等,故构成的三角形为等边三角形,画出图形可知,a,b夹角为6Oo的补角,即为12Oo;Ia+bI=Ia-bI=2IaI表示对角形相-I-—F-等的矩形,且对角线长度等于某一边长的2倍,a,b夹角为9Oo。故选Co例2、(2017,金台区期末改编)已知O为三角形ABC所在平面内一点,满足,昏h-rh-hIOB-OCI=IOB+OC-2OAI,则AABC一定是()A、等腰直角三角形B、直角三角形C、等腰三角形D、等边三角形・■■<■■■sito■BIb【解析】:IOB-OCI=IOB+OC-2OAI,nICBI=IOB-OA+OC-OAI=IAB+ACI,即对角线相等,对角线相等的平行四边形是矩形,所以AABC一定是直角三角形,选Bo平面向量系列几何意义法解题2srirD、I2aI
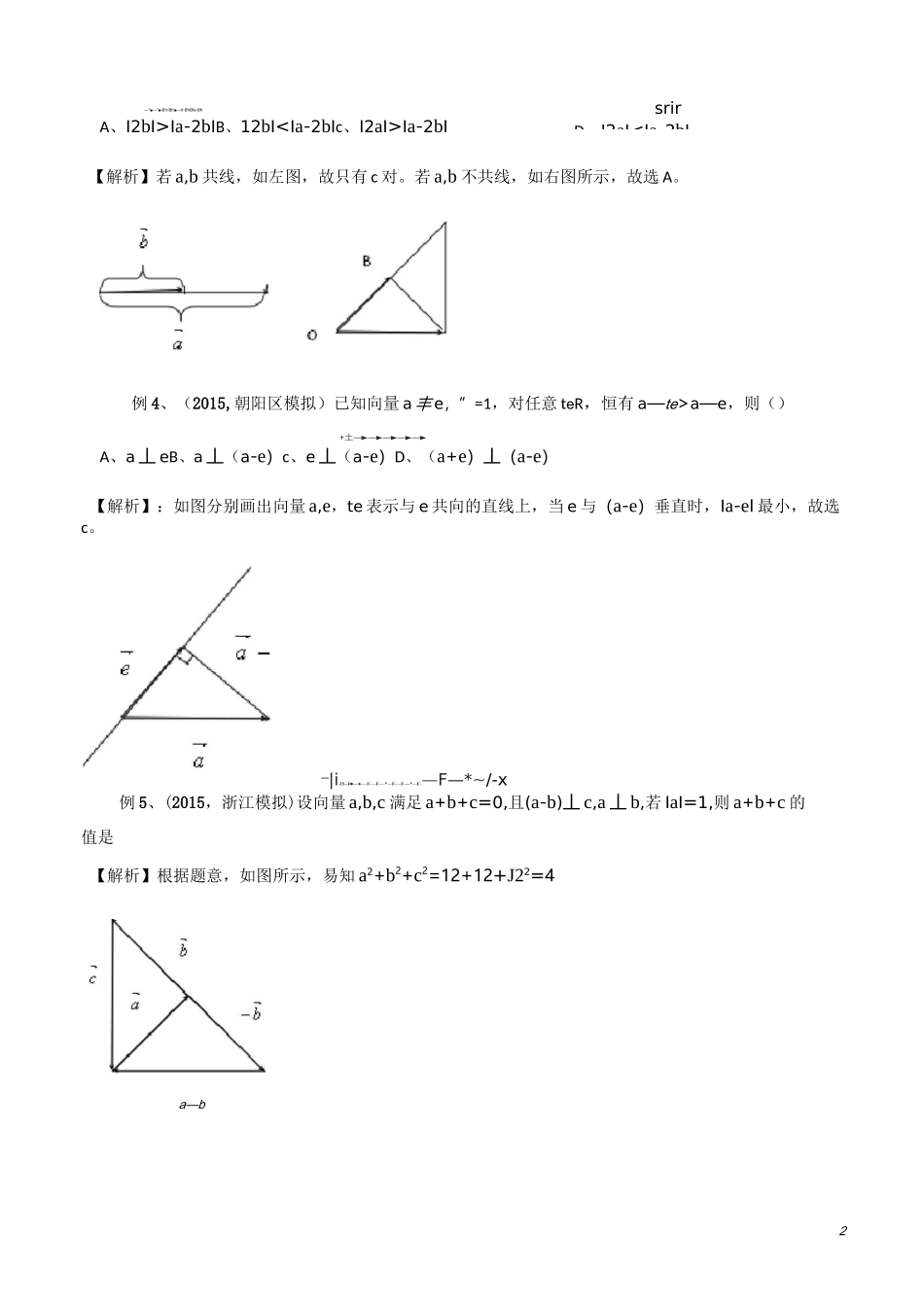
Ia-2bIB、12bIIa-2bI【解析】若a,b共线,如左图,故只有c对。若a,b不共线,如右图所示,故选A。例4、(2015,朝阳区模拟)已知向量a丰e,”=1,对任意teR,恒有a—te>a—e,则()+土—►—►—►—►—►A、a丄eB、a丄(a-e)c、e丄(a-e)D、(a+e)丄(a-e)【解析】:如图分别画出向量a,e,te表示与e共向的直线上,当e与(a-e)垂直时,Ia-eI最小,故选c。―|i-IS--¥■—►—F-—F-—*—F-—F-—*—F-—F—*~/-x例5、(2015,浙江模拟)设向量a,b,c满足a+b+c=0,且(a-b)丄c,a丄b,若IaI=1,则a+b+c的值是【解析】根据题意,如图所示,易知a2+b2+c2=12+12+J22=4a—b例6、设a,b是单位向量,a-b二o,向量c满足ic—a—bi=1,则ici的最大值为3B*1!—■!—■!BB*j【解析】IC—a—b1=1c—(a+b)l=1,根据题意,如图所示,易知IcI的最大值为血+1例6、设a,b是单位向量,a-b二o,向量c满足ic—a—bi=1,则ici的最大值为4例6、设a,b是单位向量,a-b二o,向量c满足ic—a—bi=1,则ici的最大值为5例8、(2017,吴川校级模拟)设向量a,b满足IaI=IbI=Ia+bI=1,则Ia—tbI,(teR)的最小值是.【解析】根据题意,画出图形,易知Ia—tbI=尊min26ffI——►■++例9、(2017,湛江校级月考)已知向量a,b满足Ia1=2,1b1=1,且对一切实数x,Ia+xb1>1a+bI恒成立,贝y=3兀【解析】根据题意,作出图形,易知=--;4例10、(2017,西安模拟)若两个非零向量a,b满足Ia+bI=Ia-bI=2IaI,则向量a+b与a-b的夹角是【解析】根据题意,对角线长度等于其中一条边的2倍,如图所示,易知两对角线的夹角为600。1例11、(2017,宜宾一模)设向量a,b,c满足IaI=IbI=1,a-b=-—,=60。,则IcI的最大值是【解析】根据题意,知圆内接四边形,如图所示,易知IcI为直径时最大,即IcI=2。78、巩固练练习1、(2013,清浦区校级期末)已知非零向量a,b,满足Ia1=1a+b1=1,a与b夹角为12Oo,则|b丨=【解析】作出图形可知,有一个夹角为1200的平行四边形,则将平行四边形分为两个正三角形,故有ibI=Iai=i练习2、(2016,湛江校级期末)已知向量a,b满足IaI=4,且Ia+b1=1a-bI=5,则Ib丨=【解析】:Ia+bI=Ia-bI=5n对角线等于5的矩形,又知一边为4,则另一边等于3。练习3、(2014,宝山区二模)已知i,j是方向分别与x轴和y轴正方向相同的两个基本单位向量,则平面向量Ii+jI=。【解析】i,j是互相垂直的单位向量,在平面直角坐标系中作...