动力计算概述VIP免费

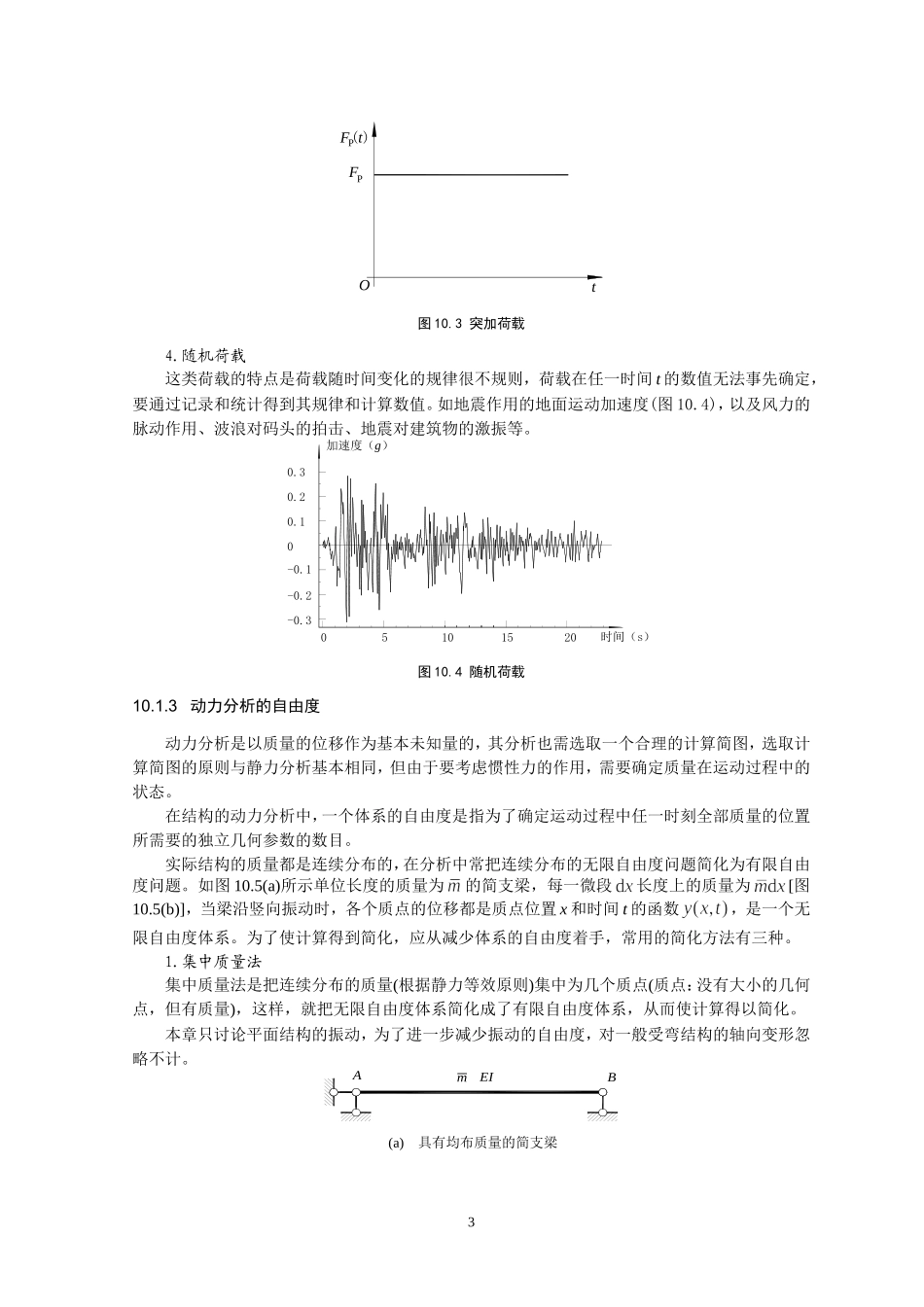
第10章结构的动力分析教学提示：本章讨论结构的动力分析，以前各章讨论的都是结构的静力分析。教学时要注意动与静、动力分析与静力分析之间的联系和区别。一方面，进行动力分析要以静力分析的有关知识作为基础。另一方面，与静力分析相比，动力分析又有许多新特点。例如，荷载、内力、位移都是时间的函数，时间是一个新的自变量；质量、惯性力、阻尼力等都是新出现的重要物理量；频率、振型、特征问题、共振现象等都是新出现的重要概念。学习时应着重掌握这些新内容。本章学习的主要内容有动力分析的特点和动力自由度，单自由度体系的自由振动，单自由度体系的受迫振动，阻尼对振动的影响，多自由度体系的自由振动，多自由度体系主振型的正交性和主振型矩阵，多自由度体系在简谐荷载下的受迫振动，多自由度体系在一般动荷载下的受迫振动，无限自由度体系的自由振动，近似法求自振频率。教学要求：学生要掌握动力分析的基本方法及体系动力自由度数的判别方法；掌握单自由度和两个自由度体系运动方程的建立方法，及其自由振动和在简谐荷载作用下受迫振动的计算方法；了解阻尼的作用；了解多自由度体系在一般动荷载作用下的受迫振动；了解频率的近似计算方法。10.1动力分析的特点和动力自由度10.1.1结构动力分析的特点前面各章讨论的是结构的静力分析问题，即结构在静力荷载作用下的内力和位移计算问题；本章讨论结构的动力分析问题，即结构在动力荷载作用下的内力和位移(常称为动力反应)计算问题。1.动力荷载的特点(1)静力荷载：荷载(大小、方向、作用位置)不随时间而变化，或随时间极其缓慢地变化(质点被近似视为在常力作用下作匀速运动，适用于惯性定律，即牛顿第二定律)，以致所引起的结构质量的加速度()及其惯性力()可以忽略不计。如活动人群、雪载、吊车荷载以及在梁上砌砖等。(2)动力荷载(也称干扰力)：荷载(大小、方向、作用位置)随时间明显变化(质点在变力作用下作加速运动)，以致所引起的结构质量的加速度()及其惯性力()不可忽略。如机器的振动荷载、地震作用、爆炸荷载等。(3)二者的主要区别：是否考虑惯性力的影响。(4)实际荷载处理：荷载随时间变化快慢是相对的，是相对于结构自振周期而言的。当荷载变化缓慢时，其变化周期远大于结构的自振周期，动力作用很小，为简化计算，将它作为静力荷载处理。当荷载过于激烈时，动力作用比较明显的荷载，惯性力不可忽略，则按动力荷载考虑。2.动力反应的特点动力反应与结构本身的动力特性有关。因此，在计算动力反应之前，必须先分析结构的自由振动，以确定结构的动力特性。3.动力分析方法的特点(1)动力分析要考虑惯性力。1(2)动内力、动位移统称动力反应，动力反应不仅是位置的函数，同时也是时间的函数。(3)在结构振动时，结构物是不平衡的，根据达朗伯原理，在引进惯性力后，可以建立动力平衡方程，将动力分析的问题转化为静力平衡问题来处理。但这只是一种形式上的平衡，仅仅是利用平衡这一手段列出运动方程。10.1.2动力荷载的分类根据动力荷载随时间变化的规律以及对结构作用的特点，工程中常见的动力荷载可分为以下几类。1.周期荷载这类荷载随时间作周期性的变化。周期荷载中最简单也是最重要的一种称为简谐荷载，即荷载随时间t的变化规律可用正弦或余弦函数表示，如图10.1(b)所示。例如具有旋转部件的机器做等速运转时，其偏心质量产生的离心力对结构的影响。具有偏心质量的机器[图10.1(a)]运转时，传到结构上的偏心力随时间t的变化规律可用或表示。F(t)=FsintPPF(t)PPFOt角速度F=FsintPyPPPxF=Fcost离心力F=meP2Oe=tmF(t)=FsintPPF(t)PPFOt角速度F=FsintPyPPPxF=Fcost离心力F=meP2Oe=tm(a)机器运转(b)简谐荷载图10.1周期荷载2.冲击荷载这类荷载在很短时间内，荷载值急剧增大[图10.2(a)]或急剧减小[图10.2(b)]。也就是很快地把全部量值加于结构而作用时间很短即行消失的荷载。各种爆炸荷载属于这一类。再如：打桩机的桩锤对桩的冲击，车轮对轨道接头处的撞击等。F(t)PPF(t)FPPFdttdttOO(a)地面爆炸(b)空中爆炸图10.2冲击荷载3.突加荷载当升载时间趋于零时，即以某...