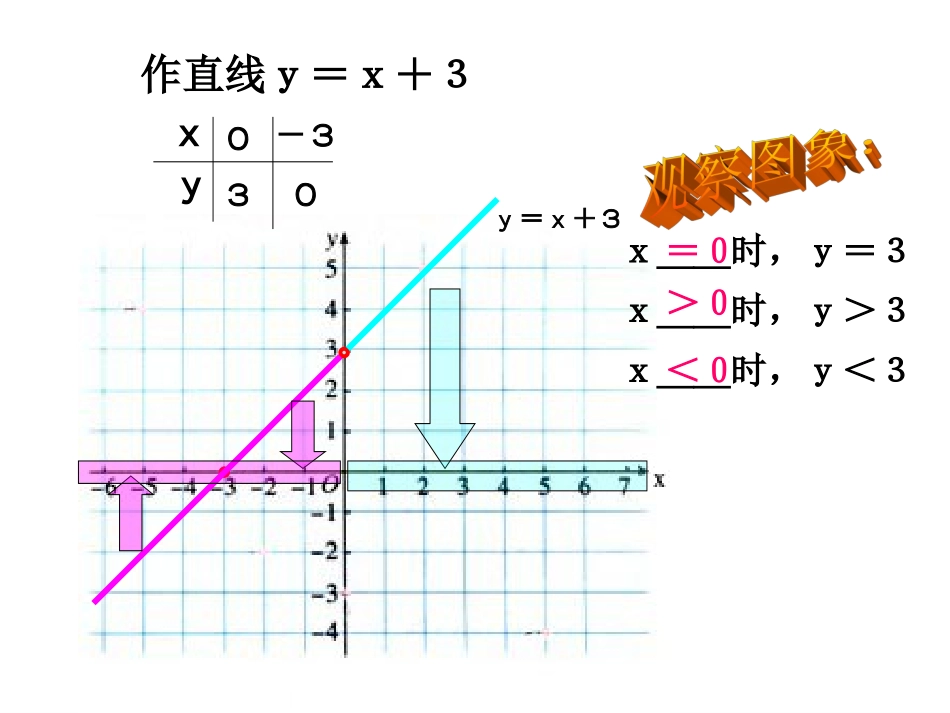
1.理解从函数的角度看解一元一次不等式.2.会根据图像解决一元一次不等式及一元一次不等式组求解的问题。学习目标:作直线y=x+3xy003-3y=x+3x__时,y>3x__时,y<3x__时,y=3=0>0<0用函数观点看不等式一次函数与一元一次不等式x的.的.求自变量求自变量的值或的值或baxy(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数x结论:因为任何一个以结论:因为任何一个以为未知数的一元为未知数的一元一一bax>0或>0或次不等式都可以变形为次不等式都可以变形为bax<0<0时,时,大于0大于0小于0小于0取值范围取值范围作直线y=x+3xy003-3y=x+3x__时,y>2x__时,y<2x__时,y=2=-1>-1<-1作直线y=2强化训练轴上方时轴上方时上的点在上的点在1、直线1、直线1xyxA.x>1B.x≥1C.x<1D.x≤1A.x>1B.x≥1C.x<1D.x≤1对应的自变量的范围是()对应的自变量的范围是()2、已知直线2、已知直线kxy2(-2,0),(-2,0),则关于不等式kx2<0<0集是()集是()的解的解A.x>-2B.x≥-2C.x<-2D.x≤-2A.x>-2B.x≥-2C.x<-2D.x≤-2轴的交点为轴的交点为与与xCCAA新课引入研读课文展示目标归纳小结课题例题:用画函数图象的方法解不等式5x+4<2x+10解法1:原不等式化为:3x-6<0,画出直线y=3x-6(如图)即这时y=3x-6<0用函数观点看不等式一次函数与一元一次不等式所以不等式的解集为:x<2x<2解法二:画出函数y=2x+10和y=5x+4图象从图中看出:即直线y=5x+4在y=2x+10的___方不等式5x+4<2x+10∴不等式5x+4<2x+10的解集是x<2x<2用函数观点看不等式一次函数与一元一次不等式思路:不等式5x+4<2x+10可以看成是两个函数值y之间的大小比较,具体在图象上是两条直线间的位置关系。下yy11yy22当当yy11=y=y22时,时,x___x___当当yy11>y>y22时,时,x___x___当当yy111<1=1yy11yy22<1>1基础练习,提高能力x<-2X>-2X>-2