第四章 理想流体动力学基本方程(Y)VIP免费

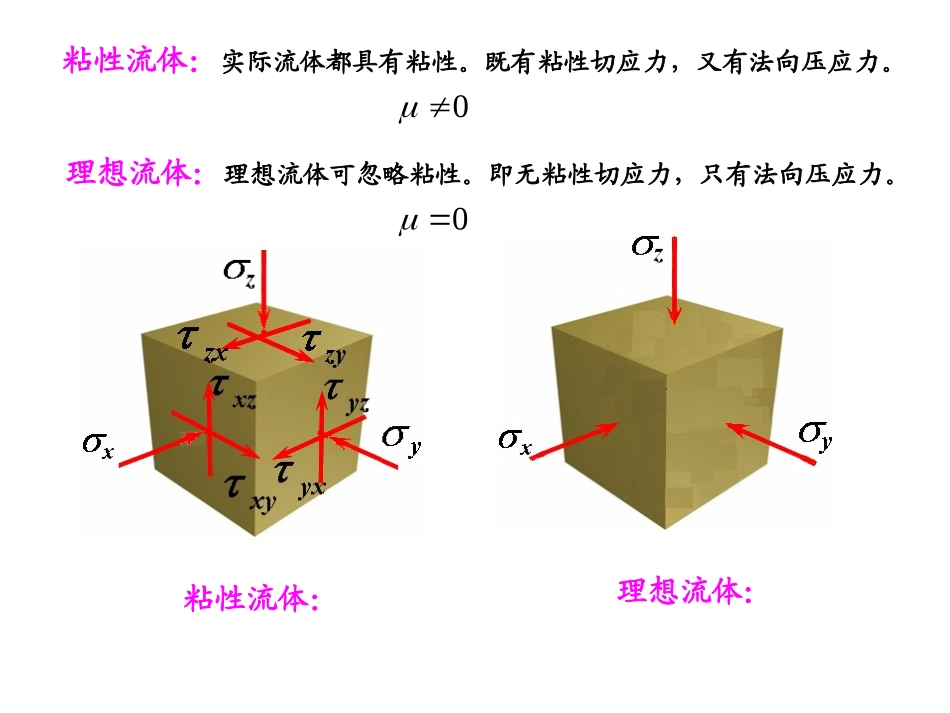
一、动量方程——流体的运动方程二、能量方程——伯努利方程三、恒定总流能量方程应用四、恒定总流动量方程与能量方程的综合应用第四章理想流体动力学基本方程主要内容主要内容动量方程：反映了流体的动量变化与外力之间的关系能量方程：机械能守恒定理粘性流体：实际流体都具有粘性，致使所研究的问题比较复杂。理想流体：指粘性为零的流体，实际上并不存在，但在有些问题中，粘性的影响很小，可以忽略不计，致使所研究的问题简单化。理想流体动力学规律可以应用于粘性的影响很小的实际流体中，所以本章的研究具有实际意义。0粘性流体：实际流体都具有粘性。既有粘性切应力，又有法向压应力。粘性流体：理想流体：理想流体：理想流体可忽略粘性。即无粘性切应力，只有法向压应力。0一、动量方程——流体的运动方程1、积分形式的动量方程——流体的运动方程质点系的动量定理：系统的动量对时间的变化率等于作用于该系统上所有的外力之合。FdtKddvvmKinii1FdvdtdAndAvdtddtd把动量代入输运方程的随体导数公式AndAvvdtvdvdtd)(FdvdtdFdAvvdtvAn)(Fdvdtd控制体τ（t）内动量随时间的变化率与单位时间内经过控制体表面A（t）流出的动量之和等于作用于控制体上所有外力之和。v作用于控制体上的外力：质量力表面力表面力：对于理想流体表面力只有压力，粘性剪应力为零。dAnpA——指外法线方向，负号表示压力n质量力：用f表示，具有加速度的量纲dfdAnpfdFdAvvdtvAAn)(——积分形式的动量方程FFdAvvdtvAn)(（1）定常流动：动量不随时间变化dAnpfddAvvdtvAAn0)(单位时间内流出控制体的动量等于作用于控制体上的外力之和——积分形式的动量方程dAnpfddAvvdtvAAn)(控制体τ（t）内动量随时间的变化率与单位时间内经过控制体表面A（t）流出的动量之和等于作用于控制体上所有外力之和。2、微分形式的动量方程——欧拉运动微分方程理想流体，无粘性切应力，只有法向压应力0坐标：x、y、z平均密度：ρ动压强：p速度：zyxuuu、、方向沿坐标轴的正向取六面体的流体微团为控制体，其边长分别为：dx、dy、dzC点（六面体的中心点）:x轴方向受到的表面压力：dxdydzxpdydzdxxppdydzdxxpp22流体微团受到x轴方向的质量力：dxdydzfx单位质量力为：kfjfiffzyxx轴方向受到的表面压力：dxdydzxpdydzdxxppdydzdxxpp22dxdydzfx根据牛顿第二定理：xxFmadxdydzfdxdydzxpdtdudxdydzxxxpfdtduxx1流体微团受到x轴方向的质量力：根据牛顿第二定理：FamzzyyxxFmaFmaFmaxxFma（1）（2）yyFmaypfdtduyy1（3）zzFmazpfdtduzz1微分形式的动量方程或欧拉运动微分方程xpfdtduxx1根据欧拉法求导：zuuyuuxuutudtduzpfzuuyuuxuutudtduypfzuuyuuxuutudtduxpfzzzyzxzzzyzyyyxyyyxzxyxxxxx111写成矢量的形式：uutudtudpf1kzjyix——哈密顿算子xpfdtduxx1ypfdtduyy1zpfdtduzz1kzjyixkujuiuuzyx（1）达朗伯原理：单位质量流体的质量力、表面力及惯性力三力组成平衡力系。011dtudpfdtudpf单位质量流体的表面力单位质量流体的惯性力单位质量流体的质量力（2）动量定理：单位质量流体...