第二章 流体静力学VIP免费

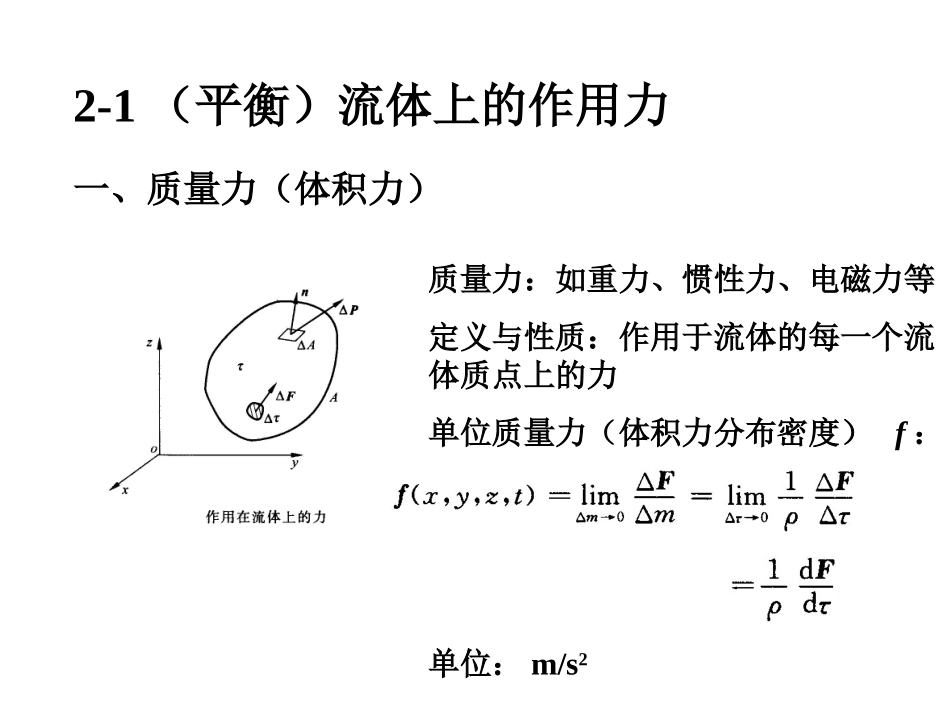
第二章流体静力学1.流体静力学的研究内容2.静止的概念和分类3.静止流体的特点2-1（平衡）流体上的作用力一、质量力（体积力）质量力：如重力、惯性力、电磁力等定义与性质：作用于流体的每一个流体质点上的力单位质量力（体积力分布密度）f：单位：m/s2二、表面力表面力：压力、粘性切应力定义性质：与接触面积有关，与流体质量体积无关。应力：单位：N/m2=Pa注意：1.下标n的意义2.pn的分解：法向应力、切向应力说明静止（平衡）流体的情况静压强静压力问题1：比较重力场（质量力只有重力）中，水和水银所受的单位质量力f水和f水银的大小？答：一样。问题2：重力场中静止的流体受到哪几种力的作用？答：重力与压力（压强），无法承受剪切力。问题3：重力场中理想流体受到哪几种力的作用？答：重力与压力，因为无粘性，故无剪切力。流体静压强及其特性静压强：在静止或相对静止的流体中，单位面积上作用的静压力称为静压强。特性一：流体静压强对某面的作用而产生的静压力必指向作用面的内法线方向。特性二：静止流体内任意一点处，压强的大小与作用面的方位无关，即同一点各方向的流体静压强均相等。dxdypPdxdzpPdydzpPzszysyxsx212121nnsndApP表面力：质量力：x方向上的力平衡方程0xF0),cos(6121xPdApdxdydzfdydzpsnnnxxdydzxPdAsnn21),cos(得同理nxppnznypppp,zyxdxdydzfdxdydzfdxdydzf61,61,61),,(zyxpp结论：压强的大小与作用面的空间方位无关，只是该点空间坐标的函数，即静压强不是一个矢量，而是一个标量。2-2流体平衡的微分方程式01ypY图2-3六面体微团ydxdzdyypp)21(dxdzdyypp)21(根据平衡条件，在y方向有，即：0yF同理：01,01zpfxpfzxfydxdydz0)21()21(ydxdydzfdxdzdyyppdxdzdyypp10ypfy流体平衡微分方程（即欧拉平衡方程）：意义：1.平衡流体中普遍适用的一个基本公式，无论平衡流体受的质量力有哪种类型，流体是否可压缩，流体有无粘性，欧拉平衡方程式都是普遍适用的。2.方程式表明：平衡流体受哪个方向的质量分量，则流体静压强沿该方向必然发生变化；反之，如果哪个方向没有质量分力，则流体静压强在该方向上必然保持不变。010101zpfypfxpfzyx将平衡方程式分别乘以dx、dy及dz，然后相加得对于不可压流体，如果单位质量力与某一个坐标函数U(x，y，z)具有下列关系W(x，y，z)是一个决定流体质量力的函数，称为力势函数，而具有这样的力势函数的质量力称为有势的力。流体只有在有势的质量力的作用下才能保持平衡。)(1)(1dzfdyfdxfdpdpdzzpdyypdxxpdzfdyfdxfzyxzyx流体平衡微分方程的综合式zWfyWfxWfzyx,,dWdp等压面：流体中压强相等各点所组成的平面或曲面叫等压面，等压面上p=const，即dp=0，则等压面微分方程式等压面三个性质：1.等压面也是等势面。2.通过任意一点的等压面必与该点所受质量力相垂直。3.两种互不相混的流体处于平衡状态时，它们的分界面必为等压面。0dzfdyfdxfzyx2-3重力场中的平衡流体重力作用下静止流体单位质量力：代入流体平衡方程式得：gdzdp对于不可压缩流体＝const，上式积分得：Cgzp设z=H时，p=p0（图），则积分常数C为：gHpC0代入原式得：ghpzHgpp00)(h为液体中任一点距液面的垂直液体深度，又称淹深。——不可压缩性流体的静压强基本公式或静液压强基本公式。0xf0yfgfz结论：（1）在重力作用下，液体内的静压强只是坐标轴z的函数，压强随深度h的增大而增大。（2）静压强由两部分组成，即液面压强p0和液体自重gh引起的压强。液面压强是外力施加于液体而引起的，可通过固体、气体或不同质的液体对液面施加外力而产生压强。（3）当h=const时，p=C，即等压面是水平面。（4）连通容器内同一种液体内与液面平行的面上具有相等的压强，这个面称为等压面。（5）帕斯卡压强传递原理：密封容器中的静止流体，由于部分边界上承受外力而产生的流体静压强，...