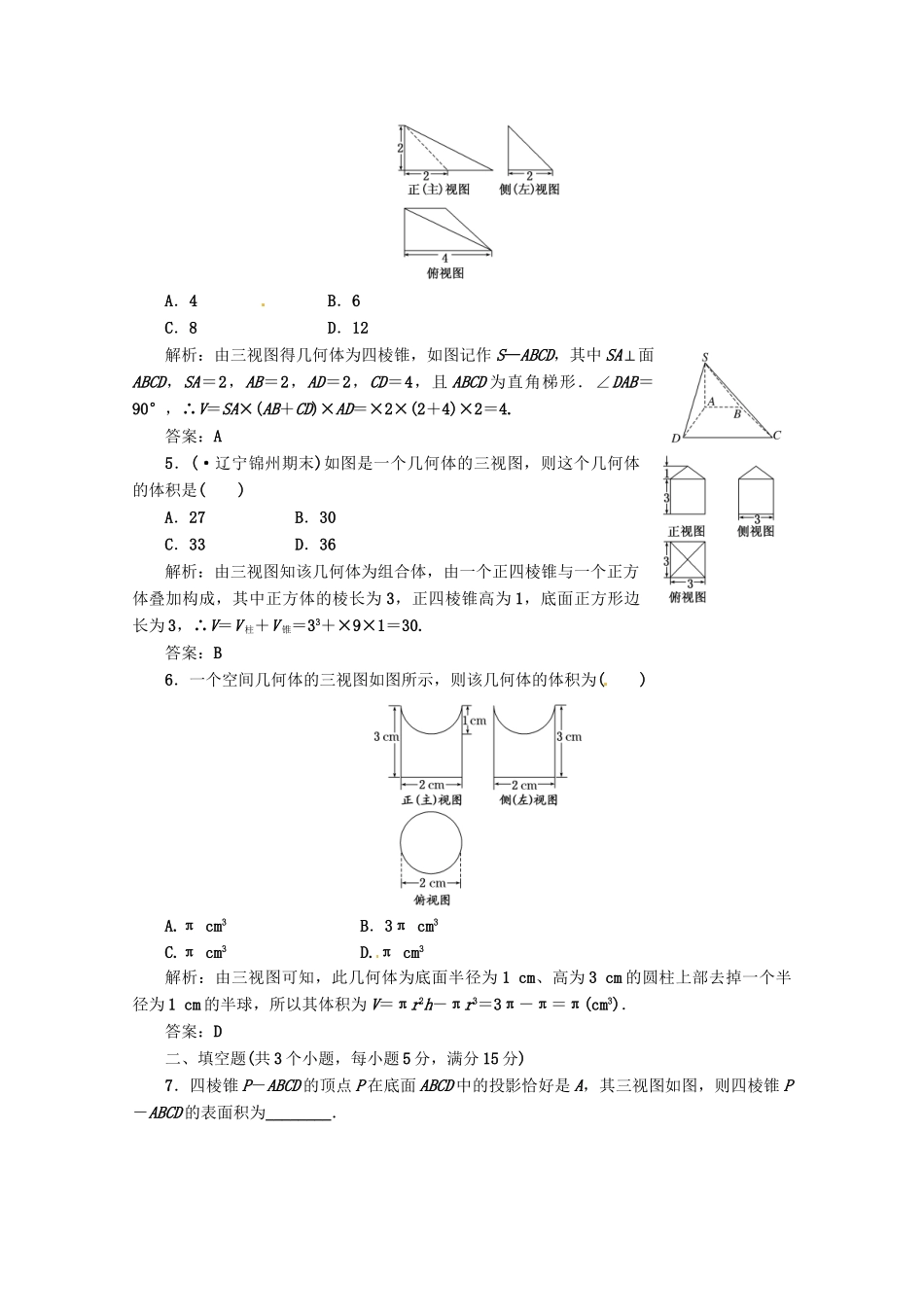
第7章第2节(时间60分钟,满分80分)一、选择题(共6个小题,每小题5分,满分30分)[来源:Z+xx+k.Com]1.(·山东潍坊)如图是一个空间几何体的三视图,这个几何体的体积是()A.2πB.3πC.6πD.9π解析:由三视图可知,该几何体是一个由底面半径为2高为3的圆柱中间挖去一个底面半径为1的等高圆柱后余下的部分,所以,其体积为π×(22-12)×3=9π.答案:D2.一个几何体的三视图及部分数据如图所示,侧(左)视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于()A.B.C.D.解析:由题中的三视图可知,该几何体是一个四棱锥,所以其体积为V=Sh=××2=.答案:A3.(·深圳模拟)如图,一个简单组合体的正(主)视图和侧(左)视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为的圆(包括圆心).则该组合体的表面积等于()A.15πB.18πC.21πD.24π解析:由题意可知,该组合体的下面为圆柱体,上面为圆锥体,由相应几何体的面积计算公式得,该组合体的表面积为:S=πr2+2πrh+πrl=π()2+2π×()×2+π×()×2=21π.答案:C[来源:学科网]4.一个几何体的三视图如图所示,则这个几何体的体积等于()A.4B.6C.8D.12解析:由三视图得几何体为四棱锥,如图记作S—ABCD,其中SA⊥面ABCD,SA=2,AB=2,AD=2,CD=4,且ABCD为直角梯形.∠DAB=90°,∴V=SA×(AB+CD)×AD=×2×(2+4)×2=4.答案:A5.(·辽宁锦州期末)如图是一个几何体的三视图,则这个几何体的体积是()A.27B.30C.33D.36解析:由三视图知该几何体为组合体,由一个正四棱锥与一个正方体叠加构成,其中正方体的棱长为3,正四棱锥高为1,底面正方形边长为3,∴V=V柱+V锥=33+×9×1=30.答案:B6.一个空间几何体的三视图如图所示,则该几何体的体积为()A.πcm3B.3πcm3C.πcm3D.πcm3解析:由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=πr2h-πr3=3π-π=π(cm3).答案:D二、填空题(共3个小题,每小题5分,满分15分)7.四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图,则四棱锥P-ABCD的表面积为________.解析:由三视图可得,三角形ABP的面积等于三角形ADP的面积且为a2,三角形BPC的面积等于三角形CDP的面积且为a2,正方形ABCD的面积为a2,所以可得四棱锥P-ABCD的表面积为(2+)a2.答案:(2+)a28.(·湖北高考)圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.解析:设球的半径为rcm,则底面圆的半径为rcm,从而有8πr2+3×πr3=6r·πr2,由此解得r=4.答案:49.(·南京模拟)如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为5cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为________cm.解析:根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为=13cm.答案:13三、解答题(共3个小题,满分35分)10.已知某几何体的俯视图是如图所示的矩形,正(主)视图是一个底边长为8,高为4的等腰三角形,侧(左)视图是一个底边长为6,高为4的等腰三角形.(1)求该几何体的体积V;(2)求该几何体的侧面积S.解:由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥.(1)V=×(8×6)×4=64.(2)该四棱锥有两个侧面PAD、PBC是全等的等腰三角形,且BC边上的高为h1==4,另两个侧面PAB、PCD也是全等的等腰三角形,AB边上的高为h2==5,因此S=2(×6×4+×8×5)=40+24.11.正三棱锥的高为1,底面边长为2,内有一个球与四个面都相切,求棱锥的表面积和球的半径.解:过PA与球心O作截面PAE与平面PCB交于PE,与平面ABC交于AE,因△ABC是正三角形,易知AE即是△ABC中BC边上的高,又是BC边上的中线,作为正三棱锥的高PD通过球心,且D是三角形△ABC的重心,据此根据底面边长为2,即可算出DE=AE=××2=,PE==,由△POF∽△PED,知=,∴=,r=-2.∴S表=S侧+S底=3××2×+×(2...