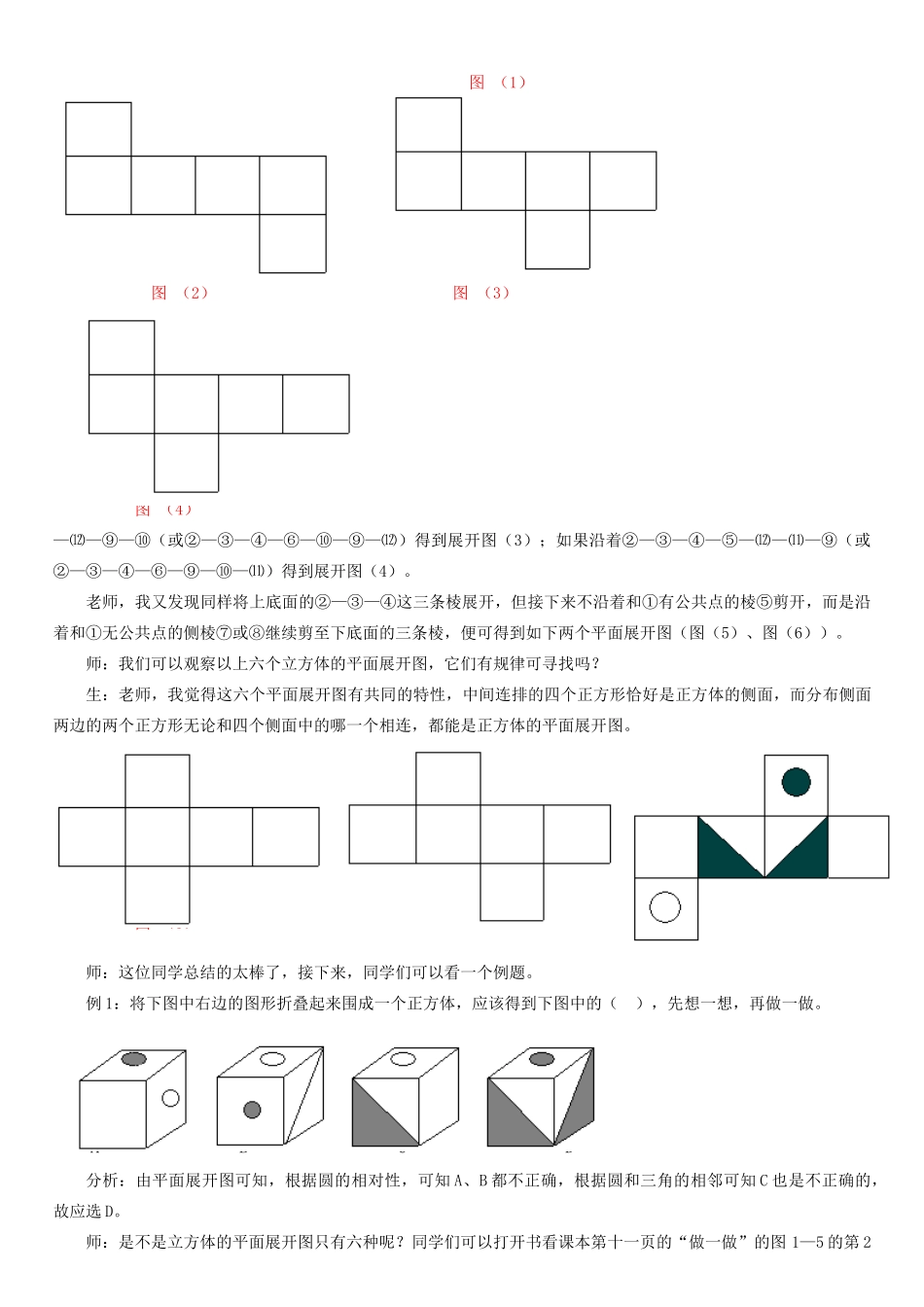
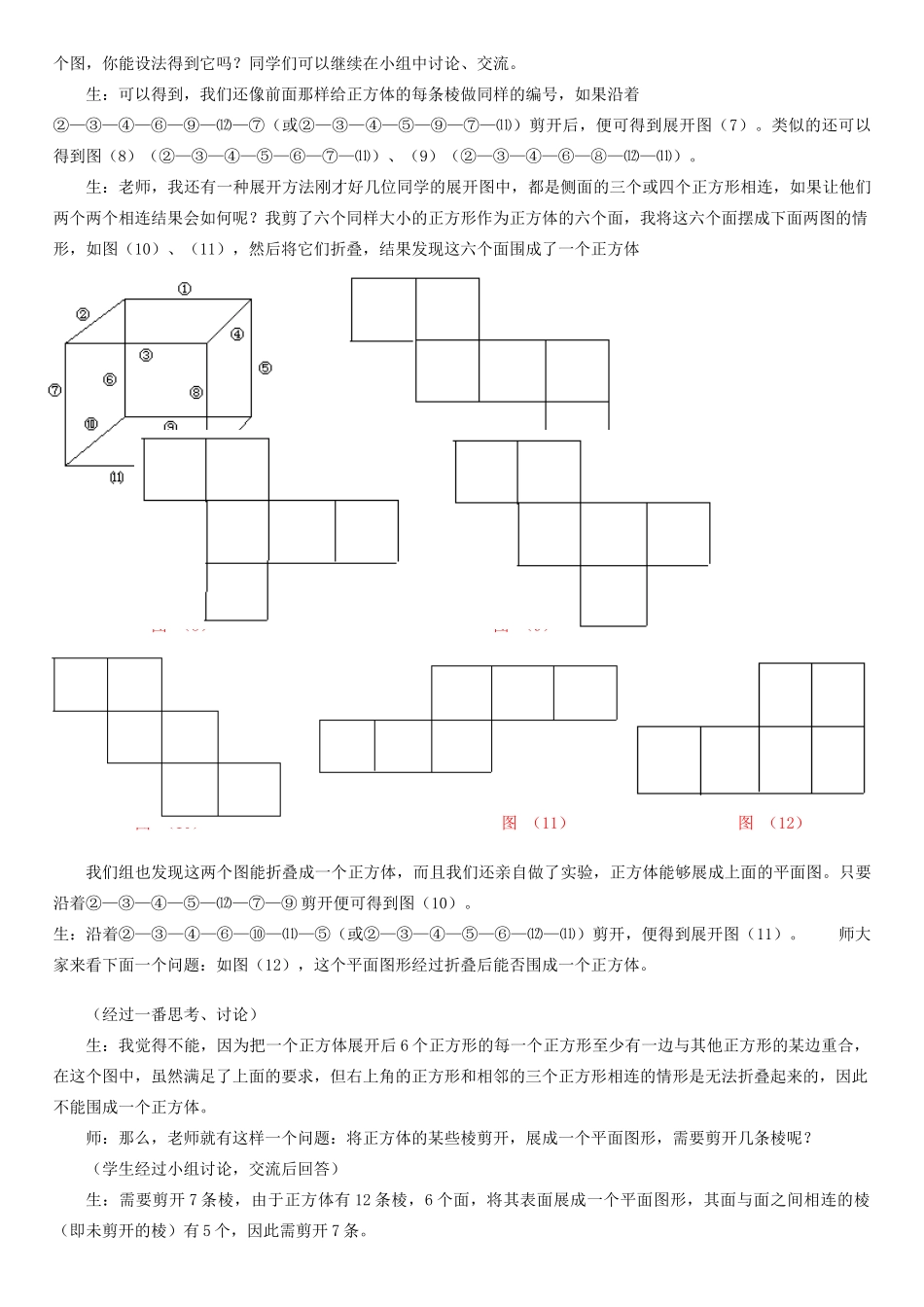
第四课时展开与折叠(2)教学目标知识要求:通过实践将一个正方体的表面沿某些棱剪开,展成一个平面图形;了解圆柱、圆锥的侧面展开图,能根据展开图判断和制作简单的立体图形。能力要求:经历展开与折叠、模型制作等活动发展空间观念,培养学生的空间想象力及操作动手能力,并积累数学活动和探究立体图形和平面图形内在联系的经验。情感与价值观要求:充分经历实践、探索、交流,获得成功的体验,。教学重点:将一个正方体的表面沿某些棱展开,展成平面图形;圆柱、圆锥的侧面展开图。教学难点:尽可能多地将一个正方体展成平面图形,开用语言描述其过程。教学方法:主体参与操作实践法。鼓励学生进行想像,并动手操作进行尝试,在操作过程中,启发学生思考,使学生操作与思考相结合。教学过程:一、创设情景,引发探究在课本第十页习题`1、3中,第1题和第2题都可以根据所给的图形折叠成六棱柱、三棱柱以及四棱柱,但如果给出一个几何体,例如我们最熟知的的正方体如果沿某些棱剪开,会得到什么样的平面图形?这样的平面图形有多少种呢?下面我们就来通过具体操作的思考来回答这个问题。二、做一做——动手实践、展示交流操作提示:1、平面展开图:将正方体展成一个平面图形,是指正方形的六个面展开后所成的六个正方形中的每一个至少有一条边与其他的正方形的某条边重合,即“相连”。2、操作提示:将一个正方体的表面沿某些棱剪开,展成一个平面图形,在操作过程中,思考下列几个问题:(1)你能得到哪些平面图形?与同伴进行交流。(2)你能设法得到图(1)—(4)中的平面图形吗?学生活动:先将上底面中的四条棱中剪开三条,然后沿着和连着的棱有公共点的侧棱顺次剪下去,到达下底面,然后再将下底面的四条棱中剪开三条,便可得到正方体的平面展开图。如图,我们给正方体的12条棱进行编号,如果沿着棱②—③—④—⑥—⑨—⑿—⑾(或②—③—④—⑤—⑨—⑩—⑾)剪开,得到展开图(1);如果如果沿着②—③—④—⑥—⑨—⑿—⑾展开,得到展开图(2);如果沿着②—③—④—⑤图(1)图(1)图(2)图(3)图(4)—⑿—⑨—⑩(或②—③—④—⑥—⑩—⑨—⑿)得到展开图(3);如果沿着②—③—④—⑤—⑿—⑾—⑨(或②—③—④—⑥—⑨—⑩—⑾)得到展开图(4)。老师,我又发现同样将上底面的②—③—④这三条棱展开,但接下来不沿着和①有公共点的棱⑤剪开,而是沿着和①无公共点的侧棱⑦或⑧继续剪至下底面的三条棱,便可得到如下两个平面展开图(图(5)、图(6))。师:我们可以观察以上六个立方体的平面展开图,它们有规律可寻找吗?生:老师,我觉得这六个平面展开图有共同的特性,中间连排的四个正方形恰好是正方体的侧面,而分布侧面两边的两个正方形无论和四个侧面中的哪一个相连,都能是正方体的平面展开图。图(5)图(6)师:这位同学总结的太棒了,接下来,同学们可以看一个例题。例1:将下图中右边的图形折叠起来围成一个正方体,应该得到下图中的(),先想一想,再做一做。ABCD分析:由平面展开图可知,根据圆的相对性,可知A、B都不正确,根据圆和三角的相邻可知C也是不正确的,故应选D。师:是不是立方体的平面展开图只有六种呢?同学们可以打开书看课本第十一页的“做一做”的图1—5的第2个图,你能设法得到它吗?同学们可以继续在小组中讨论、交流。生:可以得到,我们还像前面那样给正方体的每条棱做同样的编号,如果沿着②—③—④—⑥—⑨—⑿—⑦(或②—③—④—⑤—⑨—⑦—⑾)剪开后,便可得到展开图(7)。类似的还可以得到图(8)(②—③—④—⑤—⑥—⑦—⑾)、(9)(②—③—④—⑥—⑧—⑿—⑾)。生:老师,我还有一种展开方法刚才好几位同学的展开图中,都是侧面的三个或四个正方形相连,如果让他们两个两个相连结果会如何呢?我剪了六个同样大小的正方形作为正方体的六个面,我将这六个面摆成下面两图的情形,如图(10)、(11),然后将它们折叠,结果发现这六个面围成了一个正方体图(7)图(8)图(9)图(10)图(11)图(12)我们组也发现这两个图能折叠成一个正方体,而且我们还亲自做了实验,正方体能够展成上面的平...