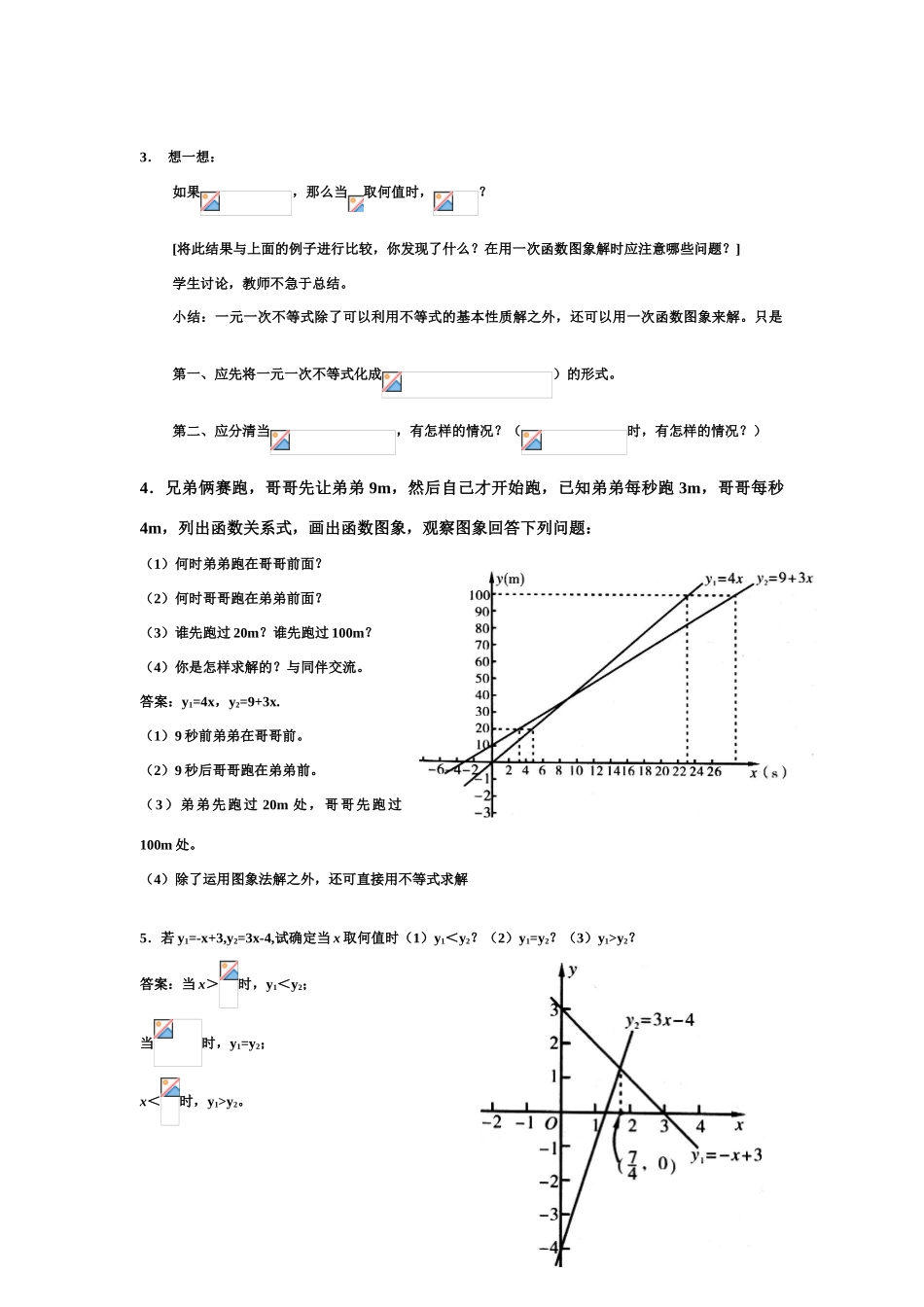
§1.5一元一次不等式与一次函数1修改07。3。2教学目的和要求:1、通过作函数图象,观察函数图象,进一步理解函数概念,并从中初步体会一元一次不等式与一次函当的内在联系。2、通过具体问题初步体会一次函数的变化规律与一次函数的变化规律与一元一次不等式解集的联系。教学重点和难点:重点:先建立函数模型,再建立不等式模型。难点:沿着“读题---建立模型---求解模型---解释”的思路让学生主动思考1.快速反应:指出函数y=3x-6的自变量与因变量,并作出其图象,用图象法求出当x取何值时,(1)3x-6>0(2)3x-6<0用直接解不等式的方法求上题中的有两个不等式的解集,并比较两种方法的结果相同吗?(或设置情境小明听了爸爸的字如其人的一番教诲,想到自己龙飞凤舞的“草书”作品连自己都认不出来的笑话,下决心练字,在第一周的前3天每天练字6页。设每周计划练字x页。你能写出x与y之间的关系式吗?这是一个什么函数?若周计划为页,则x取怎样的值,小明才能超额完成计划?)2.自主学习:1.作出函数y=2x-5的图象,观察图象回答下列问题:(1)x取哪些值时,2x-5>0?(2)x取哪些值时,2x-5<0?(3)x取哪些值时,2x-5>3?答案:(1)当x>2.5时,2x-5>0。(2)当x<2.5时,2x-5<0(3)当x>4时,2x-5>3。3.想一想:如果,那么当取何值时,?[将此结果与上面的例子进行比较,你发现了什么?在用一次函数图象解时应注意哪些问题?]学生讨论,教师不急于总结。小结:一元一次不等式除了可以利用不等式的基本性质解之外,还可以用一次函数图象来解。只是第一、应先将一元一次不等式化成)的形式。第二、应分清当,有怎样的情况?(时,有怎样的情况?)4.兄弟俩赛跑,哥哥先让弟弟9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒4m,列出函数关系式,画出函数图象,观察图象回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?(3)谁先跑过20m?谁先跑过100m?(4)你是怎样求解的?与同伴交流。答案:y1=4x,y2=9+3x.(1)9秒前弟弟在哥哥前。(2)9秒后哥哥跑在弟弟前。(3)弟弟先跑过20m处,哥哥先跑过100m处。(4)除了运用图象法解之外,还可直接用不等式求解5.若y1=-x+3,y2=3x-4,试确定当x取何值时(1)y1<y2?(2)y1=y2?(3)y1>y2?答案:当x>时,y1<y2;当时,y1=y2;x<时,y1>y2。6.甲、乙两辆摩托车从相距20km的A、B两地相向而行,图中l1、l2分别表示两辆摩托车离开A地的距离s(km)与行驶时间t(h)之间函数关系。a)哪辆摩托车的速度较快?b)经过多长时间,甲车行驶到A、B两地中点?解答:(1)从图象中可知∴故摩托车乙速度快。(2)当s=10km时,,即经过0.3h时,甲车行驶到A、B两地的中点。7.学生若干人,住若干间宿舍,如果每间住4人,则余19人没有住处,如果每间住6人,则有一间宿舍不空也不满,求有多少间宿舍?多少个学生?答案:房间有10间或11间或12间,学生有59人或63人或67人。8.中国第三届京剧艺术节在南京举行,某场京剧演出的票价由2元到100元多种,某团体须购买票价为6元和10元的票共140张,其中票价为10元的票数不少于票价为6元的票数的2倍。问这两种票各购买多少张所需的钱最少?最少需要多少钱?答:购买46张6元票,94张10元票所花的钱最少,最少需要1216元。