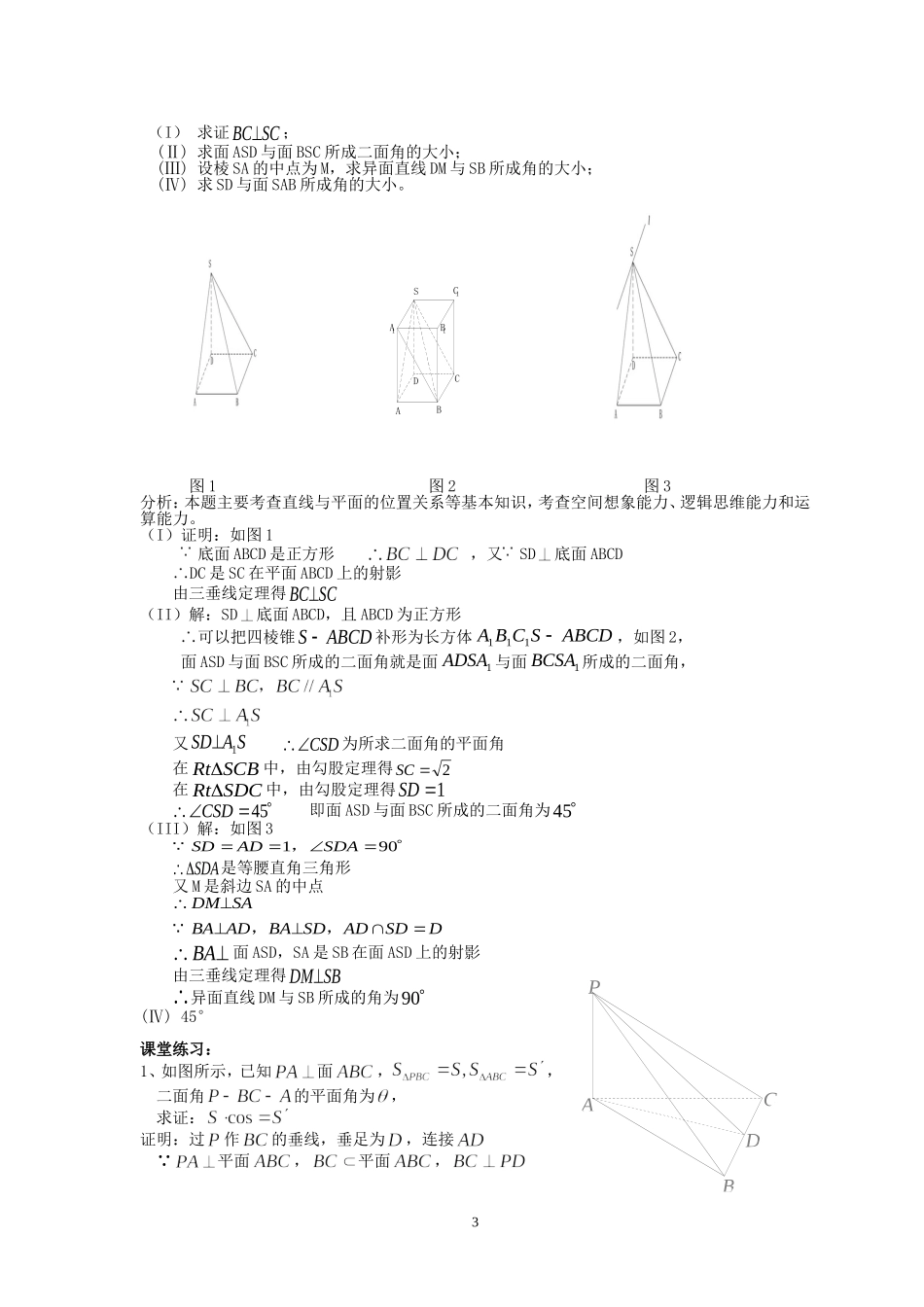
OCBAODCBA空间角李小昌教学目的1.理解并掌握斜线在平面内的射影、异面直线所成的角、直线和平面所成角的概念。2.根据概念、先找直线射影、后确定线面夹角,从而熟练求解直线和平面所成角。3.理解二面角及其平面角的概念,能确认图形中的已知角是否为二面角的平面角。4.掌握二面角的平面角的一般作法:(1)根据定义;(2)作二面角棱的垂面;(3)利用三垂线定理或逆定理。5.理解面面垂直问题可能化为线面垂直的问题。6.培养化归能力、分析能力、观察思考能力和空间想象能力等。7.培养立体感、数学美感,提高学生学习数学特别是立体几何的兴趣。教学重点1.线面夹角的概念及利用概念分步求夹角。2.二面角的概念和二面角的平面角的作法。教学难点1.直线和平面所成角的概念及的应用。2.二面角的平面角的一般作法及其寻求。授课类型复习课课时安排2课时教具多媒体、实物投影仪教学过程第一课时引入新课:高考立体几何试题一般共有4道(客观题3道,主观题1道),共计总分27分左右,考查的知识点在20个以内.选择填空题考核立几中的计算型问题,而解答题着重考查立几中的逻辑推理型问题,当然,二者均应以正确的空间想象为前提.随着新的课程改革的进一步实施,立体几何考题正朝着”多一点思考,少一点计算”的发展.从历年的考题变化看,以多面体和旋转体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题。例1、如图,已知是平面的一条斜线,为斜足,为垂足,为内的一条直线,,求斜线和平面所成角。解: ,由斜线和平面所成角的定义可知,为和所成角,又 ,∴,∴,即斜线和平面所成角为.例2、已知空间四边形的各边及对角线相等,求与平面所成角的余弦值奎屯王新敞新疆解:过作平面于点,连接,∴即为与平面所成角, ,∴是正三角形的外心,设四面体的边长为,则,1 ,∴,所以,与平面所成角的余弦值为.例3、如图1,直三棱柱ABC-ABC的各条棱长都相等,D为棱BC上的一点,在截面ADC中,若ADC=,求二面角D-AC-C的大小.解:由已知,直三棱柱的侧面均为正方形, ADC=90,即ADCD.又CC平面ABC,ADCC.AD侧面BC,ADBC,D为BC的中点.过C作CECD于E, 平面ADC侧面BC,CE平面ADC.取AC的中点F,连结CF,则CFAC.连结EF,则EFAC(三垂线定理)图1EFC是二面角D-AC-C的平面角.在RtEFC中,sinEFC=.设BC=CC=a易求得CE=,CF=.sinEFC=,EFC=arcsin.二面角D-AC-C的大小为arcsin.例4、四棱锥P—ABCD的底面是边长为a的正方形,PB⊥面ABCD.(1)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;(2)证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°解:(1)正方形ABCD是四棱锥P—ABCD的底面,其面积为从而只要算出四棱锥的高就行了.面ABCD,∴BA是PA在面ABCD上的射影.又DA⊥AB,∴PA⊥DA,∴∠PAB是面PAD与面ABCD所成的二面角的平面角,∴∠PAB=60°.∴PB=AB·tan60°=a,而PB是四棱锥P—ABCD的高,.(2)不论棱锥的高怎样变化,棱锥侧面PAD与PCD恒为全等三角形.作AE⊥DP,垂足为E,连结EC,则△ADE≌△CDE,是面PAD与面PCD所成的二面角的平面角.设AC与DB相交于点O,连结EO,则EO⊥AC,在故平面PAD与平面PCD所成的二面角恒大于90°.本小题主要考查线面关系和二面角的概念,以及空间想象能力和逻辑推理能力,具有一定的探索性,是一道设计新颖,特征鲜明的好题.例5、(2004年北京春季高考题)如图,四棱锥SABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=。2DCBPA(I)求证BCSC;(Ⅱ)求面ASD与面BSC所成二面角的大小;(Ⅲ)设棱SA的中点为M,求异面直线DM与SB所成角的大小;(Ⅳ)求SD与面SAB所成角的大小。C1CADBA1SB1图1图2图3分析:本题主要考查直线与平面的位置关系等基本知识,考查空间想象能力、逻辑思维能力和运算能力。(I)证明:如图1底面ABCD是正方形,又SD底面ABCDDC是SC在平面ABCD上的射影由三垂线定理得BCSC(II)解:SD底面ABCD,且ABCD为正方形可以把四棱锥SABCD补形为长方体ABCSABCD111,如图2,面ASD与面BSC所成的二面角就是面ADSA1与面BCSA1所成的二面角,又SDAS1CSD为所求二面角的平面角在RtSCB...