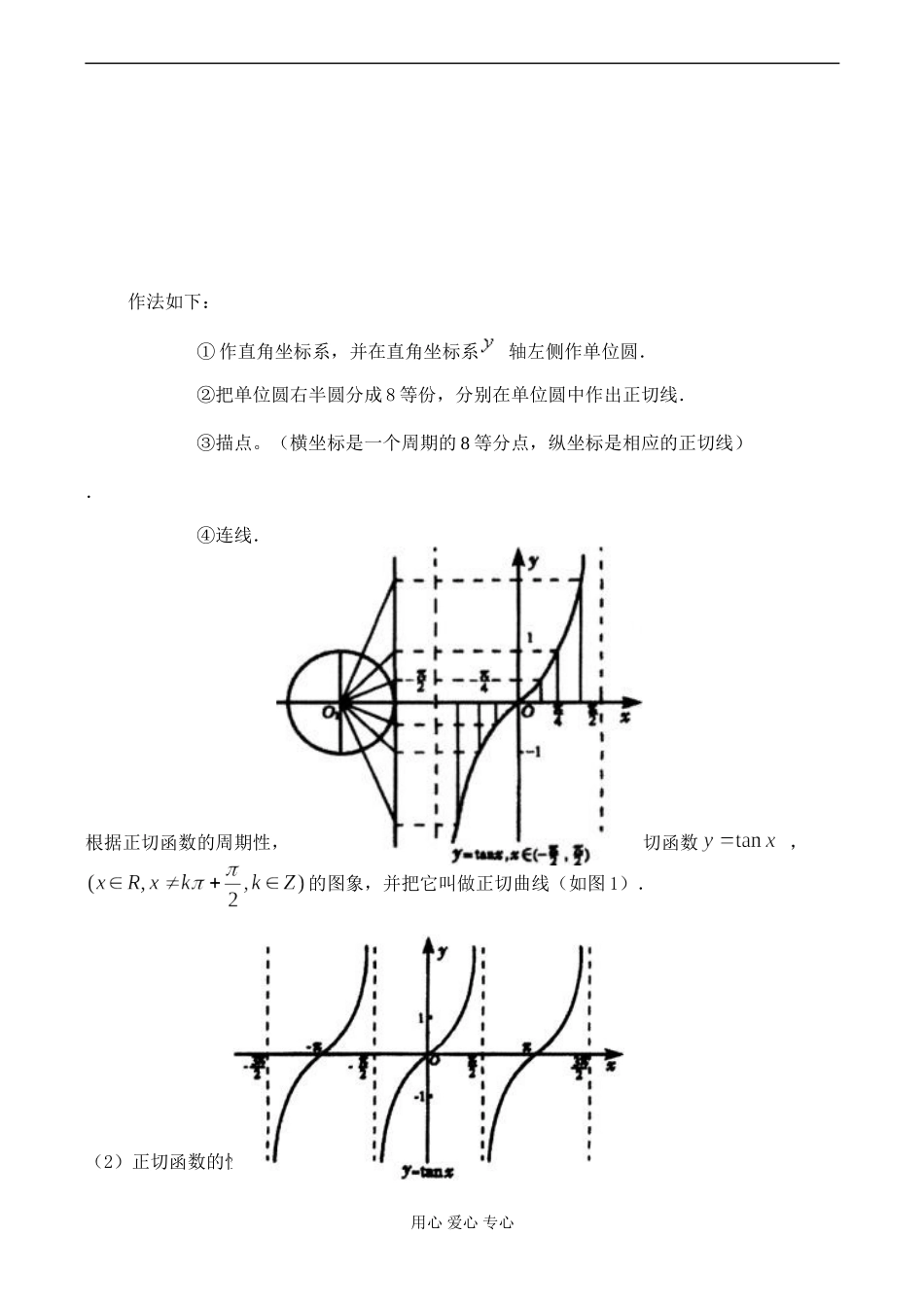
高二数学正切函数的图象和性质教材分析:学习正切函数的图象和性质,主要包括:定义域、值域、周期性、单调性、奇偶性等,以及具体的应用。(一)素质教育目标:1.知识目标:(1)用单位圆中的正切线作正切函数的图象;(2)用正切函数图象解决函数有关的性质;2.能力目标:(1)理解并掌握作正切函数图象的方法;(2)理解用函数图象解决有关性质问题的方法;3.德育目标:培养研究探索问题的能力;(二)教学三点解析:1.教学重点:用单位圆中的正切线作正切函数图象;2.教学难点:性质的研究;3.教学疑点:正切函数在每个单调区间是增函数,并非整个定义域内的增函数;(三)教学过程设计1.设置情境前面我们研究了正、余弦函数的图象和性质,但常见的三角函数还有正切函数,今天我们来探讨一下正切函数的图象,以及它具有哪些性质。2.探索研究由研究正、余弦函数的图象和性质的方法引出正切函数的图象和性质。下面我们也将利用单位圆中的正切线来绘制图象.(1)用正切线作正切函数图象分析一下正切函数是否为周期函数?∴是周期函数,是它的一个周期.我们还可以证明,是它的最小正周期.类似正弦曲线的作法,我们先作正切函数在一个周期上的图象,下面我们利用正切线画出函数,的图象.用心爱心专心作法如下:①作直角坐标系,并在直角坐标系轴左侧作单位圆.②把单位圆右半圆分成8等份,分别在单位圆中作出正切线.③描点。(横坐标是一个周期的8等分点,纵坐标是相应的正切线).④连线.图1根据正切函数的周期性,我们可以把上述图象向左、右扩展,得到正切函数,的图象,并把它叫做正切曲线(如图1).图2(2)正切函数的性质用心爱心专心请同学们结合正切函数图象研究正切函数的性质:定义域、值域、周期性、奇偶性和单调性.①定义域:②值域:③周期性:正切函数是周期函数,周期是.④奇偶性:,∴正切函数是奇函数,正切曲线关于原点对称.⑤单调性:由正切曲线图象可知:正切函数在开区间内都是增函数.强调:a.不能说正切函数在整个定义域内是增函数b.正切函数在每个单调区间内都是增函数c.每个单调区间都包括两个象限:四、一或二、三3.例题分析【例1】求函数的定义域.分析:我们已经知道了的定义域,那么与有什么关系呢?令,我们把说成由和复合而成。此时我们称为复合函数,而把和为简单函数解:令,那么函数的定义域是由,可得所以函数的定义域是用心爱心专心解题回顾:这种解法可称为换元法,因此复合函数可通过换元法来求得。练习1:求函数的定义域。(学生板演。)【例2】不通过求值,比较下列各组中两个正切函数值的大小:(1)与;(2)与.分析:比较两个正切函数值的大小可联想到比较两个正、余弦函数值的大小。比较两个正、余弦函数值的大小是利用函数的单调性来比较。注意点是应把相应的角化到正或余弦函数的同一单调区间内来解决.类比得到比较两个正切函数值的大小的解法解:(1)又∵,在上是增函数∴(2)∵=又∵0<<<,函数,是增函数,∴<即.用心爱心专心解题回顾:比较两个正切型实数的大小,关键是把相应的角诱导到的同一单调区间内,利用的单调递增性来解决.练习2:比较大小:(学生口答)(<)(学生板演)(>)【例3】求的周期3.总结提炼(1)这节课我们采用类比的思想方法来学习正切函数的图象和性质(2)正切函数的作图是利用平移正切线得到的,当我们获得一个周期上图象后,再利用周期性把该段图象向左右延伸、平移。(3)正切函数的性质.4.布置作业:作业:苏大资料“12.正切函数的图象与性质”.用心爱心专心