北师版数学必修4两角和与差的三角函数VIP免费

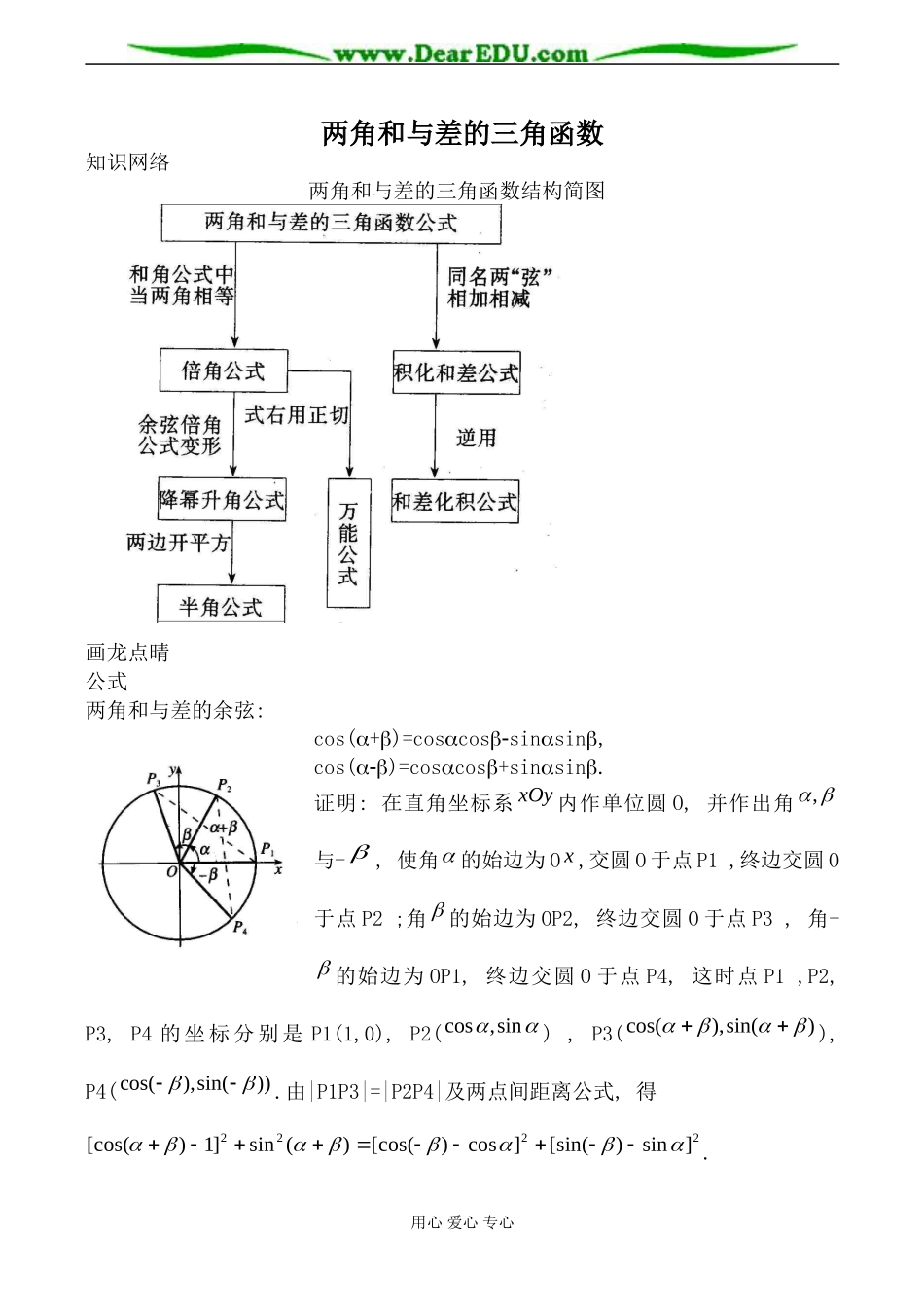
两角和与差的三角函数知识网络两角和与差的三角函数结构简图画龙点晴公式两角和与差的余弦:cos(+)=coscossinsin,cos()=coscos+sinsin.证明:在直角坐标系xOy内作单位圆O,并作出角,与-,使角的始边为Ox,交圆O于点P1,终边交圆O于点P2;角的始边为OP2,终边交圆O于点P3,角-的始边为OP1,终边交圆O于点P4,这时点P1,P2,P3,P4的坐标分别是P1(1,0),P2(sin,cos),P3()sin(),cos(),P4())sin(),cos(.由|P1P3|=|P2P4|及两点间距离公式,得2222]sin)[sin(]cos)[cos()(sin]1)[cos(.用心爱心专心展开并整理,得2-2),sinsincos(cos22)cos(所以cos(+)=coscossinsin.这个公式对于任意的角,都成立.在公式中用-代替,就得到cos(-)=coscos(-)sinsin(-),即cos()=coscos+sinsin.[活用实例][例1]计算：(1)cos65cos115cos25sin115;(2)cos70cos20+sin110sin20.[题解](1)原式=cos65cos115sin65sin115=cos(65+115)=cos180=1;(2)原式=cos70cos20+sin70sin20=cos(70+20)=0.[例2]已知sin=53，cos=1312求cos()的值.[题解] sin=53>0，cos=1312>0∴可能在一、二象限，在一、四象限若、均在第一象限，则cos=54，sin=135cos()=656313553131254;若在第一象限，在四象限，则cos=54，sin=135cos()=6533)135(53131254;若在第二象限，在一象限，则cos=54，sin=135cos()=6533135531312)54(;若在第二象限，在四象限，则cos=54，sin=135cos()=6563)135(531312)54(.[例3]已知锐角,满足cos=53cos(+)=135求cos.[题解] cos=53∴sin=54又 cos(+)=135<0∴+为钝角∴sin(+)=1312,用心爱心专心∴cos=cos[(+)]=cos(+)cos+sin(+)sin=653354131253135.两角和与差的正弦:sin(+)=sincos+cossin,sin()=sincoscossin.证明:在两角和的余弦公式中,利用诱导公式,可得到sin(+)=])2cos[()](2cos[=sin)2sin(cos)2cos(=sincos+cossin,即sin(+)=sincos+cossin.用代替上面公式中的,可得到sin(-)=sincos(-)+cossin(-),即sin()=sincoscossin.[活用实例][例4]已知sin+cos=53①,cos+sin=54②，求sin(+).[题解]①2:sin2+2sincos+cos2=259③②2:cos2+2cossin+sin2=2516④③+④:2+2(sincos+cossin)=1即：sin(+)=-21.[例5]已知sin(+)=32,sin()=52求的值.[题解] sin(+)=32∴sincos+cossin=32①sin()=52∴sincoscossin=52②①+②：sincos=158①②：cossin=152[例6]已知432，1312)cos(，53)sin(，求sin2的值.[题解] 01312)cos(432∴40∴135)sin(用心爱心专心=.∴23又：53)sin(∴54)cos(∴sin2=)sin()(0)cos()sin()]()sin[(sc=655613554131253.两角和与差的正切:tan(+)=tantan1tantan,tan()=tantan1tantan.变形：tan+tan=tan()(1-tantan).证明:cos(+)=coscossinsin,sin(+)=sincos+cossin,当0)cos(时,将两式的两边分别相除,即tan(+)=tantan1tantan,用-代替上面公式中的,得到tan()=tantan1tantan.[活用实例][例7]已知tan=31，tan=2求cot()，并求+的值，其中0<<90,90<<180.[题解]cot()=71tantantantan1)tan(1 tan(+)=1)2(3...