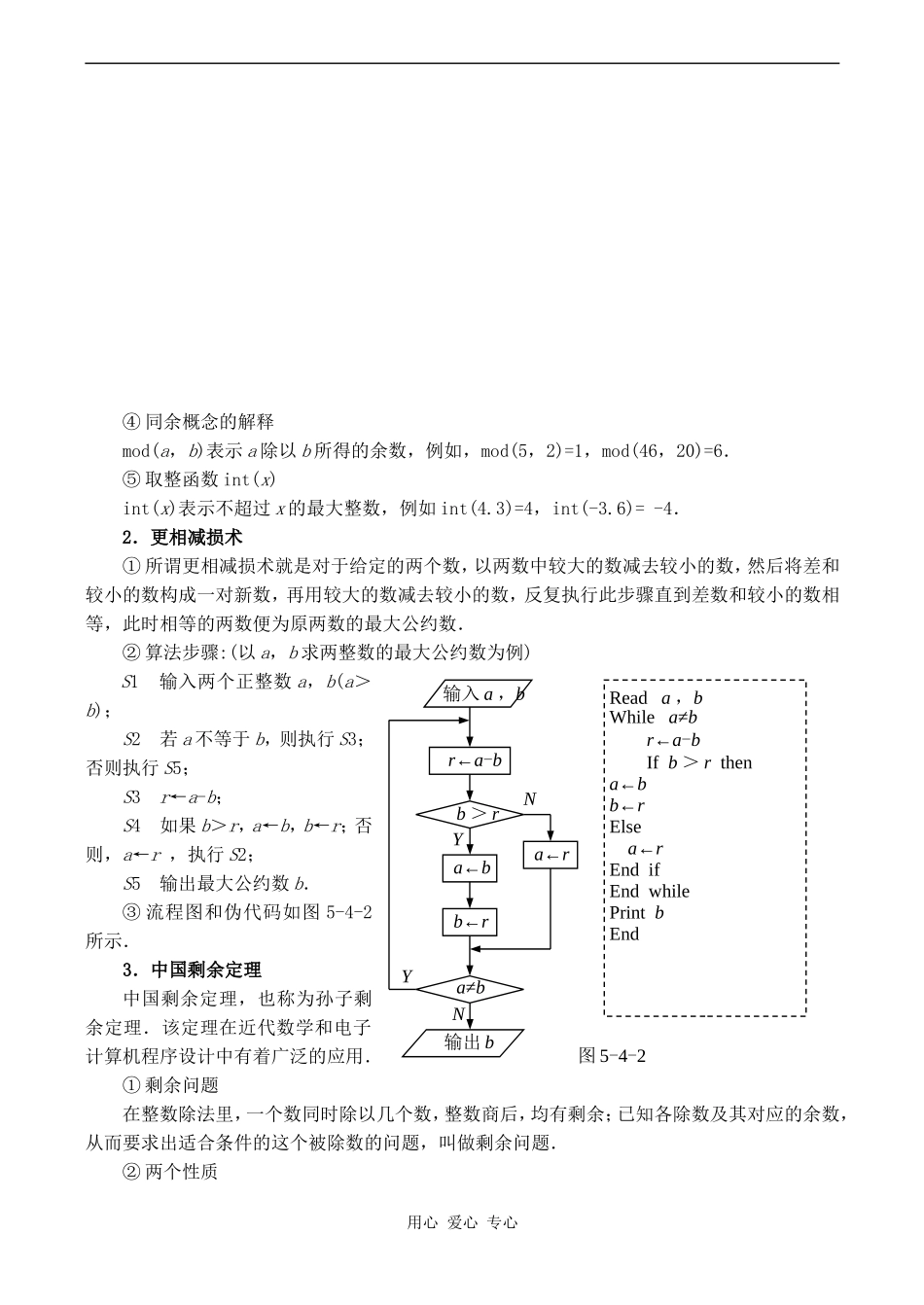
算法案例民间谚语说,不了解过去,就不可能懂得现在的真正涵义和未来的目的.这对于数学也是适用的.事实上,从世界文明古代数学到我国古代数学,它们中都蕴藏着大量丰富的“寓理于算”的引人入胜的数学问题、趣题,这些问题的“算法化”解决,可帮助同学们进一步体会“算法”的概念,提高逻辑思维能力和算法设计水平,进而为上机实践作好更为充分的准备并节省计算机资源.同时,不仅在古代,就是在当今,也有着许多充满了挑战意味的(算法)问题,值得我们去开拓去玩味去思索.现在,同学们肯定也一定很想知道到底有哪些问题是如此地吸引着我们的眼球吧.那就请你随着我们一起去走进数学问题的算法大观圆吧.学法建议“数学来源于实践”.作为算法,也不例外,它是许多优秀成果(无论是古代的,还是当今的)的浓缩、抽象与概括.追根溯源,我们再用“算法”理念来研究体验一下充满着体现古代数学对现代数学的伟大贡献的成果,那就不仅具有深远的现实意义,而且同样具有深远的教育意义.在本节的学习中,要能综合运用所学的算法知识解决实际问题,会用自然语言、流程图和伪代码表述问题的算法过程.一、知识网络对比提示南宋数学家秦九韶对《孙子算经》中的“物不知数”问题产生了兴趣并进行了研究,提出了一种新的算法——大衍求一术,该法和高斯的算法在本质上完全一致,但比高斯早了500余年,可见中国古代数学史对世界古代数学史的贡献.二、知识归纳1.辗转相除法①所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数,若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时的较小的数就是原来两个数的最大公约数.②算法步骤(以求两正整数a,b的最大公约数为例)S1输入两个正整数a,b(a>b);S2r←a÷b的余数;S3a←b;S4b←r;S5如果r=0,则输出最大公约数a;若r≠0,则转S2.③流程图与伪代码如图5-4-1所示.用心爱心专心中国剩余定理算法案例更相减损二分法辗转相除法10Reada,b20r←mod(a,b)30a←b40b←rIfr≠0then8060PrintaGoto9080Goto20Endif100EndNa←br←mod(a,b)输入a,b输出aYb←rr=0图5-4-1④同余概念的解释mod(a,b)表示a除以b所得的余数,例如,mod(5,2)=1,mod(46,20)=6.⑤取整函数int(x)int(x)表示不超过x的最大整数,例如int(4.3)=4,int(-3.6)=-4.2.更相减损术①所谓更相减损术就是对于给定的两个数,以两数中较大的数减去较小的数,然后将差和较小的数构成一对新数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原两数的最大公约数.②算法步骤:(以a,b求两整数的最大公约数为例)S1输入两个正整数a,b(a>b);S2若a不等于b,则执行S3;否则执行S5;S3r←a-b;S4如果b>r,a←b,b←r;否则,a←r,执行S2;S5输出最大公约数b.③流程图和伪代码如图5-4-2所示.3.中国剩余定理中国剩余定理,也称为孙子剩余定理.该定理在近代数学和电子计算机程序设计中有着广泛的应用.①剩余问题在整数除法里,一个数同时除以几个数,整数商后,均有剩余;已知各除数及其对应的余数,从而要求出适合条件的这个被除数的问题,叫做剩余问题.②两个性质用心爱心专心Reada,bWhilea≠br←a-bIfb>rthena←bb←rElsea←rEndifEndwhilePrintbEndr←a-b输入a,b输出bNa←r图5-4-2b>rYa←bb←rNa≠bY性质1几个数相加,如果只有一个加数,不能被数a整除,而其他加数均能被数a整除,那么它们的和,就不能被数a整除.如:10能被5整除,15能被5整除,但7不能被5整除,所以(10+15+7)不能被5整除.性质2二数不能整除,若被除数扩大(或缩小)了几倍,而除数不变,则其余数也同时扩大(或缩小)相同的倍数(余数必小于除数).如:22÷7=3……1(22×4)÷7=12……1×4(=4)(要余2:22×2÷7=6……2;(22×9)÷7=28……1×9-7(=2))(想余5,则22×5÷7=15……5)③中国剩余定理中国数学史书上记载:在两千多年前的我国古代算书《孙子算经》中,有这样一个问题(称为“物不知数”问题)及其解法:今有物不知其数,三三数之剩二;五五数之剩三:七七数之剩二.问物几何...