高中数学函数的单调性（3）——最值教案新人教版必修1VIP免费

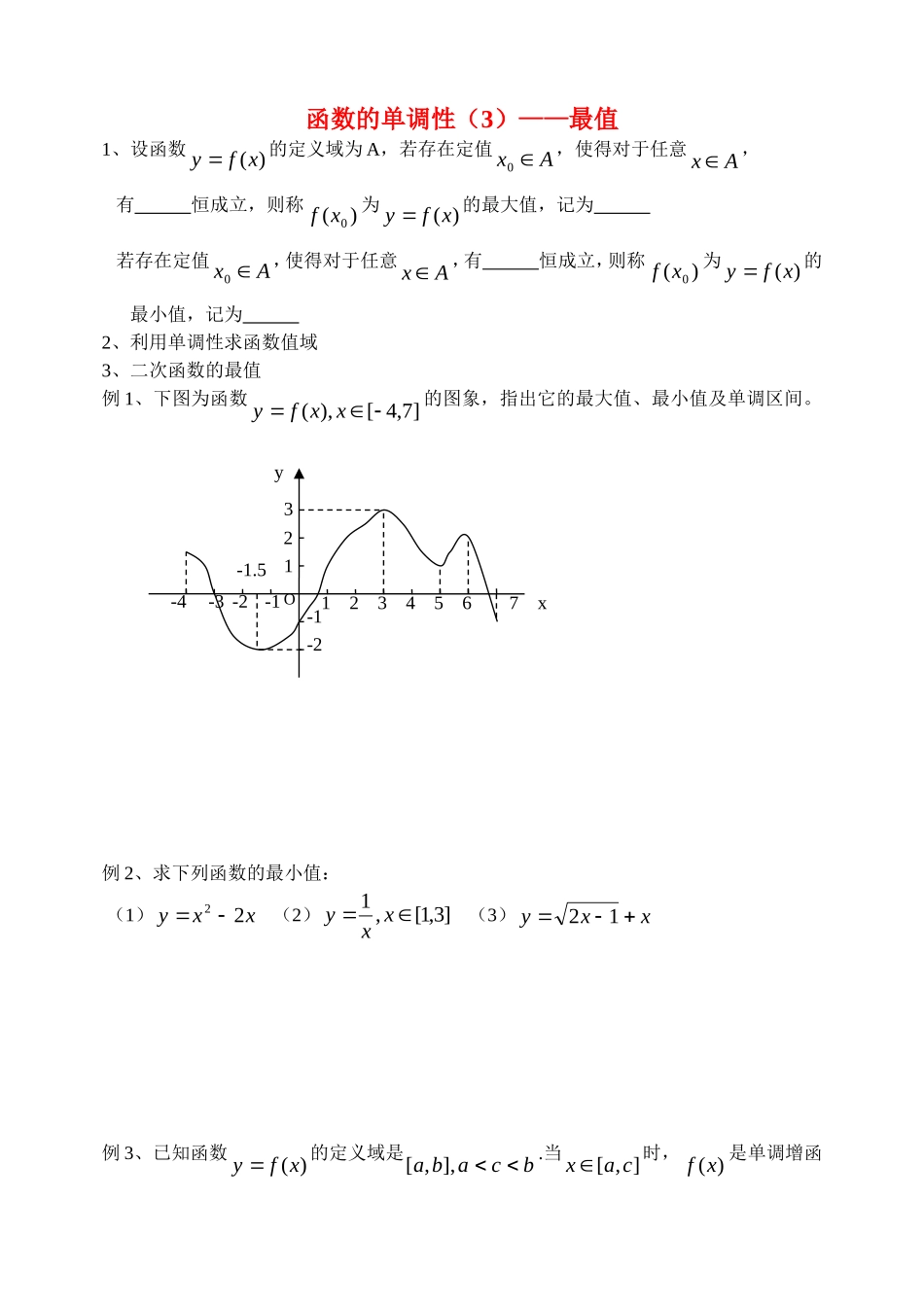
函数的单调性（3）——最值1、设函数)(xfy的定义域为A，若存在定值Ax0，使得对于任意Ax，有恒成立，则称)(0xf为)(xfy的最大值，记为若存在定值Ax0，使得对于任意Ax，有恒成立，则称)(0xf为)(xfy的最小值，记为2、利用单调性求函数值域3、二次函数的最值例1、下图为函数]7,4[),(xxfy的图象，指出它的最大值、最小值及单调区间。例2、求下列函数的最小值：（1）xxy22（2）]3,1[,1xxy（3）xxy12例3、已知函数)(xfy的定义域是bcaba],,[.当],[cax时，)(xf是单调增函yOx-1-2-1-2-4-31231234567-1.5数，当],[bcx时，)(xf是单调减函数。试证明)(xf在cx时取得最大值。例4、函数322xxy在闭区间],0[m上有最大值3，最小值2，求m的取值范围。三、巩固练习：1、书p37：3,42、函数mxxy62的最小值为1，则m的值为3、函数15103032xxxxxxy的最大值为4、)1(11)(xxxf的最大值为