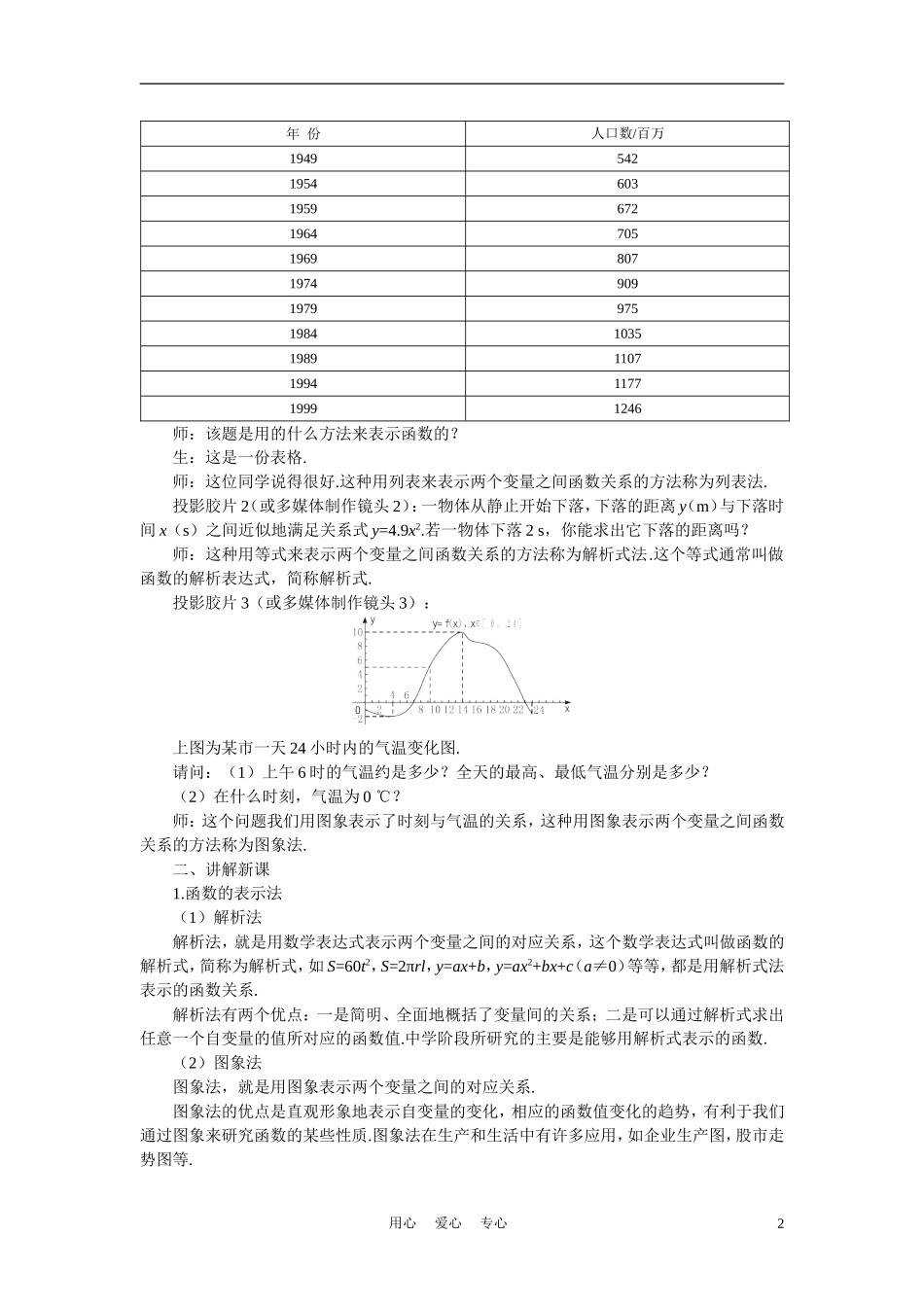
1.2.2函数的表示法(1)从容说课学习函数的表示,不仅是研究函数本身和应用函数解决实际问题所必须涉及的问题,而且是加深理解函数概念的过程.同时,基于高中阶段所接触的许多函数均可用几种不同的方式表示,因而使得学习函数的表示也是向学生渗透数形结合方法的重要过程.初中已经接触过函数的三种表示法:解析法、列表法和图象法.高中阶段是让学生在了解三种表示法各自优点的基础上,重点在于使学生面对实际情境时,会根据不同的需要选择恰当的方法(图象法、列表法、解析法)表示函数.根据实际问题中的条件列出函数解析式的训练,是建立函数模型研究实际问题的关键步骤,这种应用意识的培养和应用能力的提高应不断贯穿于以后的教学过程中.本课还介绍了分段函数,在实际问题中,有很多函数是用分段函数来表示的,所以探讨分段函数是很有必要的,在教学中结合教材内容向学生渗透分类思想方法,对培养学生全面分析问题、解决问题的能力是很有帮助的.应该说这是知识螺旋化的一种体现,教学时要让学生体会到函数三种表示法具有内在的联系,它们在一定条件下是可以相互转化的.对函数的解析式和图象表示应重点研究.三维目标一、知识与技能1.能熟练掌握函数的三种不同表示.2.了解函数不同表示法的优缺点.3.了解分段函数及其表示.4.会求某些函数的解析式.二、过程与方法1.自主学习,了解函数表示形式的多样性和转化方法.2.探究与活动,明白何时的函数用何种方法表示适宜.3.增强动态意识、通过观察、对比、分析,发展辩证思维能力.三、情感态度与价值观培养学生重要数学思想方法——数形结合与分类讨论思想方法,激发学生学习的热情.教学重点函数的三种不同表示的相互间转化.教学难点函数的解析式的表示,理解和表示分段函数.教具准备多媒体课件、投影仪、打印好的材料.教学过程一、创设情景,引入新课师:在前面的课中,我们已经初步研究函数的概念和表示方法.今天我们再专门研究函数的表示方法.(板书:函数的表示方法)师:请考察下面三个函数:投影胶片1(或多媒体制作镜头1):估计人口数量变化趋势是我们制定一系列相关政策的依据.从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如表所示,你能根据这个表说出我国人口的变化情况吗?1949~1999年我国人口数据表用心爱心专心1年份人口数/百万194954219546031959672196470519698071974909197997519841035198911071994117719991246师:该题是用的什么方法来表示函数的?生:这是一份表格.师:这位同学说得很好.这种用列表来表示两个变量之间函数关系的方法称为列表法.投影胶片2(或多媒体制作镜头2):一物体从静止开始下落,下落的距离y(m)与下落时间x(s)之间近似地满足关系式y=4.9x2.若一物体下落2s,你能求出它下落的距离吗?师:这种用等式来表示两个变量之间函数关系的方法称为解析式法.这个等式通常叫做函数的解析表达式,简称解析式.投影胶片3(或多媒体制作镜头3):上图为某市一天24小时内的气温变化图.请问:(1)上午6时的气温约是多少?全天的最高、最低气温分别是多少?(2)在什么时刻,气温为0℃?师:这个问题我们用图象表示了时刻与气温的关系,这种用图象表示两个变量之间函数关系的方法称为图象法.二、讲解新课1.函数的表示法(1)解析法解析法,就是用数学表达式表示两个变量之间的对应关系,这个数学表达式叫做函数的解析式,简称为解析式,如S=60t2,S=2πrl,y=ax+b,y=ax2+bx+c(a≠0)等等,都是用解析式法表示的函数关系.解析法有两个优点:一是简明、全面地概括了变量间的关系;二是可以通过解析式求出任意一个自变量的值所对应的函数值.中学阶段所研究的主要是能够用解析式表示的函数.(2)图象法图象法,就是用图象表示两个变量之间的对应关系.图象法的优点是直观形象地表示自变量的变化,相应的函数值变化的趋势,有利于我们通过图象来研究函数的某些性质.图象法在生产和生活中有许多应用,如企业生产图,股市走势图等.用心爱心专心2(3)列表法列表法,就是列出表格来表示两个变量之间的对应关系.列表法的优点是不需要计算就可以直接看出与自变量的值相对应的函数值,表格法在实际生产和...