高中数学 第三章《不等式》学案 北师大版必修5VIP免费

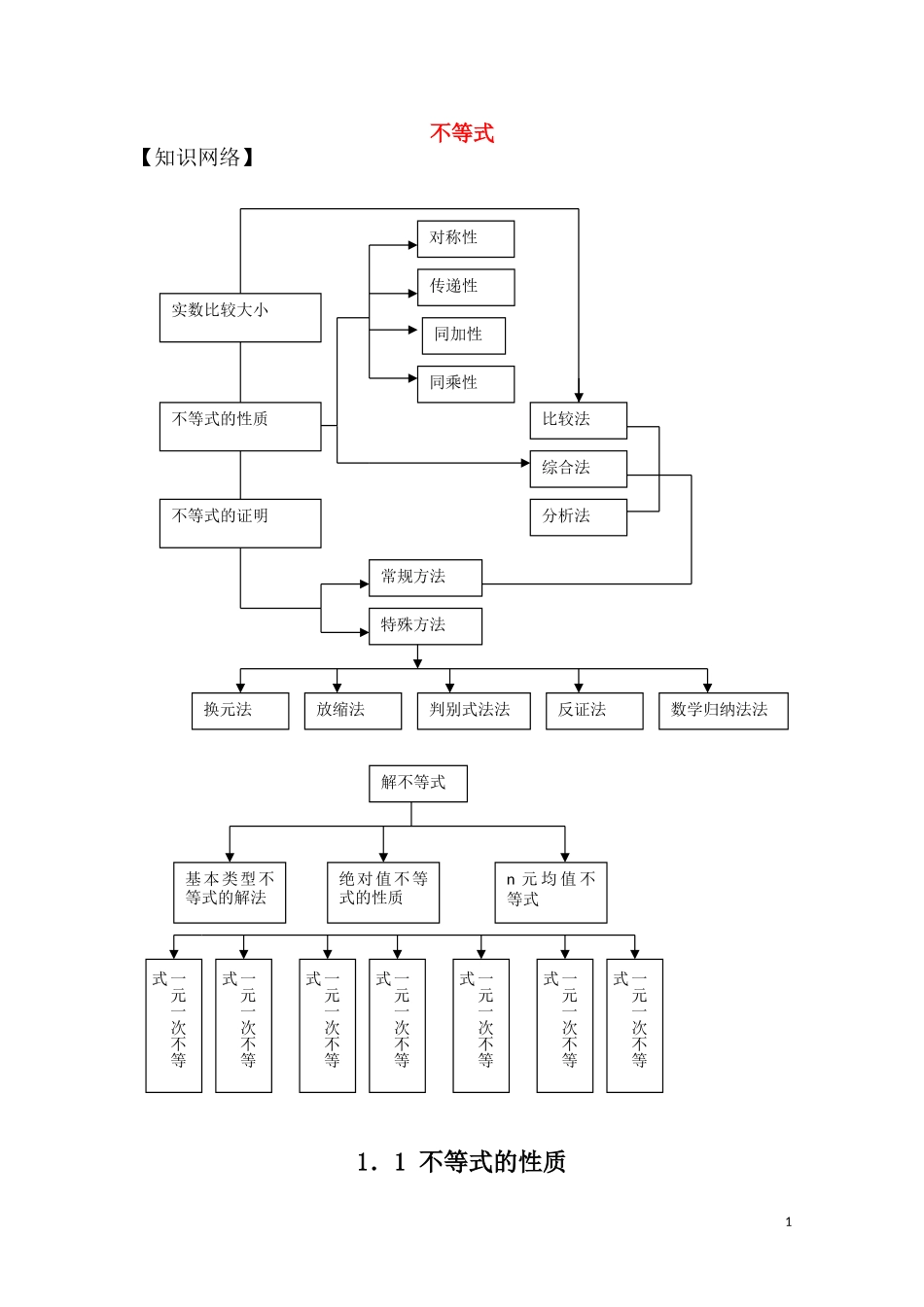
不等式【知识网络】1．1不等式的性质1同加性传递性同乘性对称性不等式的性质实数比较大小不等式的证明综合法分析法比较法常规方法特殊方法换元法放缩法判别式法法反证法数学归纳法法解不等式基本类型不等式的解法n元均值不等式绝对值不等式的性质一元一次不等式一元一次不等式一元一次不等式一元一次不等式一元一次不等式一元一次不等式一元一次不等式【考点透视】一、考纲指要1．理解不等式的性质及其证明.二、命题落点1．不等式的性质主要以客观题形式出现往往融于其他问题之中，.如例1，例22．利用不等式的性质结合已知条件比较大小、判断不等式有关结论是否成立或利用不等式研究变量的范围，求字母的取值或取值范围等..如练习9.【典例精析】例1:若0,ab则下列不等式不能成立的是（）A．11abB．22abC．0abD．11()()22ab解析:由0ab知ab>0,因此1111,abababab即成立;由0,ab得0,0;abab所以成立由于x12是减函数,所以ab1122亦成立,故一定不成立的是B．答案：B．例2：（2003•北京）设a，b，c，d∈R，且a>b，c>d，则下列结论中正确的是（）A．a+c>b+dB．a－c>b－dC．ac>bdD．cbda解析： a>b，c>d，∴a+c>b+D．答案：A．例3：（2005•福建）不等式01312xx的解集是（）A．}2131|{xxx或B．}2131|{xxC．}21|{xxD．}31|{xx解析:不等式01312xx的解是x>12或x<13.答案：A．【常见误区】1．不等式的“运算”只有加法法则和乘法法则，没有减法法则和除法法则，再利用数的性质进行转化时往往出错；2．在运用不等式的性质是对不等式进行了非同解变形.【基础演练】1．（2004•北京）已知a、b、c满足，且，那么下列选项中不一定成立的是2（）A．B．C．D．0)(caac2．（2004•湖北)若011ba，则下列不等式①abba；②|;|||ba③ba；④2baab中，正确的不等式有（）A．1个B．2个C．3个D．4个3．（2004•辽宁）对于10a，给出下列四个不等式（）①)11(log)1(logaaaa②)11(log)1(logaaaa③aaaa111④aaaa111其中成立的是（）A．①与③B．①与④C．②与③D．②与④4.对“a、b、c是不全相等的正数”，给出下列判断：①222()()()0abbcca；②a＞b与a＜b及a≠c中至少有一个成立；③a≠c，b≠c，a≠b不能同时成立．其中判断正确的个数为（）A．0个B．1个C．2个D．3个5．二次函数2()yaxbxcxR的部分对应值如下表：则不等式20axbxc的解集是_________________．6．若不等式2025axx£+-有且只有一个解，则实数a=．7．比较大小：abab与baab（0,0ab且ab）.8．已知222,1,3abcabcabc,求证12bc．9．定义在R上的函数()fx满足:如果对任意x1,x2∈R,12,xxR都有12()2xxf≤121[()()],2fxfx则称函数()fx是R上的凹函数．[来源:Z+xx+k.Com]已知二次函数2(),0fxaxxaRa求证:当0a时,函数()fx是凹函数．x-3-2-101234y60-4-6-6-40631．2算术平均数与几何平均数【考点透视】一、考纲指要1．掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用.二、命题落点1．以二元均值不等式的考查最为常见，命题形式往往在选择题或填空题中，如例1，例2，例3.2．在解答题中常与最值问题结合在一起以及函数的值域等知识一起考查，试题解法突出常规方法，淡化特殊技巧，一般以求最值的形式来问如练习题9.【典例精析】例1:（2005•全国1）当20x时，函数xxxxf2sinsin82cos1)(2的最小值为（）A．2B．32C．4D．34解析：xxxxxxxxxxxxfcossin4sincoscossin2sin8cos22sinsin82cos1)(222[来源:学科网]4cossin4sincos2xxxx，当且仅当xxxxcossin4sincos，即21tanx时，取“”， 2π0x，∴存在x使21tanx，这时4)(maxxf，答案：C．例2：(2005•福建)下列结论正确的是（）A．当2lg1lg,10xxxx时且B．21,0xxx时当C．xxx1,2时当的最小值为2D．当xxx1,20时无最大值解析：A中lgx不满足大于零,C中的最小值为2的x值取不...