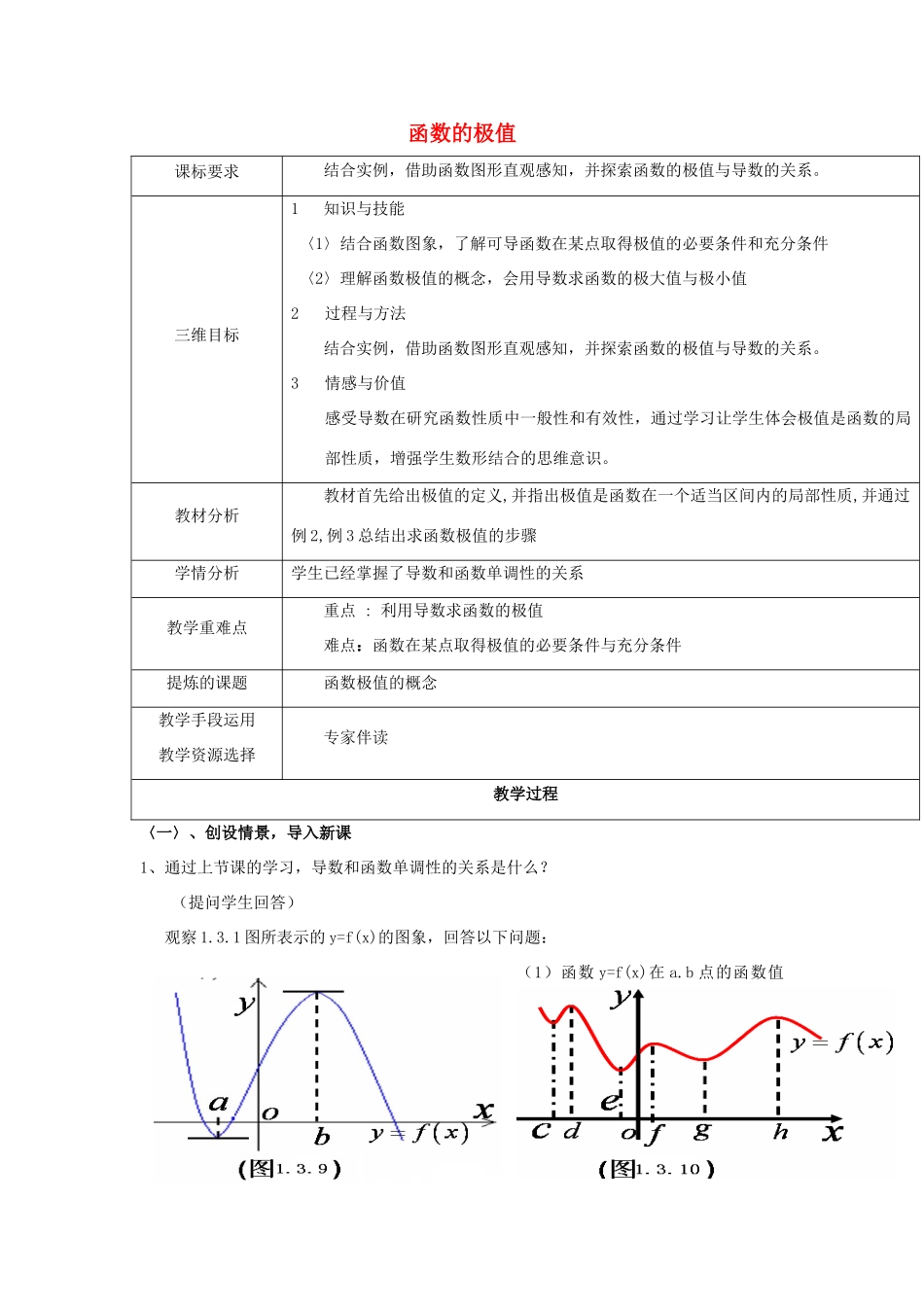
函数的极值课标要求结合实例,借助函数图形直观感知,并探索函数的极值与导数的关系。三维目标1知识与技能〈1〉结合函数图象,了解可导函数在某点取得极值的必要条件和充分条件〈2〉理解函数极值的概念,会用导数求函数的极大值与极小值2过程与方法结合实例,借助函数图形直观感知,并探索函数的极值与导数的关系。3情感与价值感受导数在研究函数性质中一般性和有效性,通过学习让学生体会极值是函数的局部性质,增强学生数形结合的思维意识。教材分析教材首先给出极值的定义,并指出极值是函数在一个适当区间内的局部性质,并通过例2,例3总结出求函数极值的步骤学情分析学生已经掌握了导数和函数单调性的关系教学重难点重点:利用导数求函数的极值难点:函数在某点取得极值的必要条件与充分条件提炼的课题函数极值的概念教学手段运用教学资源选择专家伴读教学过程〈一〉、创设情景,导入新课1、通过上节课的学习,导数和函数单调性的关系是什么?(提问学生回答)观察1.3.1图所表示的y=f(x)的图象,回答以下问题:(1)函数y=f(x)在a.b点的函数值与这些点附近的函数值有什么关系?(2)函数y=f(x)在a.b.点的导数值是多少?(3)在a.b点附近,y=f(x)的导数的符号分别是什么,并且有什么关系呢?2、极值的定义:我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;点b叫做函数y=f(x)的极大值点,f(a)叫做函数y=f(x)的极大值。极大值点与极小值点称为极值点,极大值与极小值称为极值.<三>、讲解例题例2,例3,见课本例4函数的极值归纳:求函数y=f(x)极值的方法是:1求,解方程=0,当=0时:(1)如果在x0附近的左边>0,右边<0,那么f(x0)是极大值.(2)如果在x0附近的左边<0,右边>0,那么f(x0)是极小值<四>、课堂练习1、求函数f(x)=3x-x3的极值2、思考:已知函数f(x)=ax3+bx2-2x在x=-2,x=1处取得极值,求函数f(x)的解析式及单调区间。<五>、课堂小结:1、函数极值的定义2、函数极值求解步骤3、一个点为函数的极值点的充要条件。