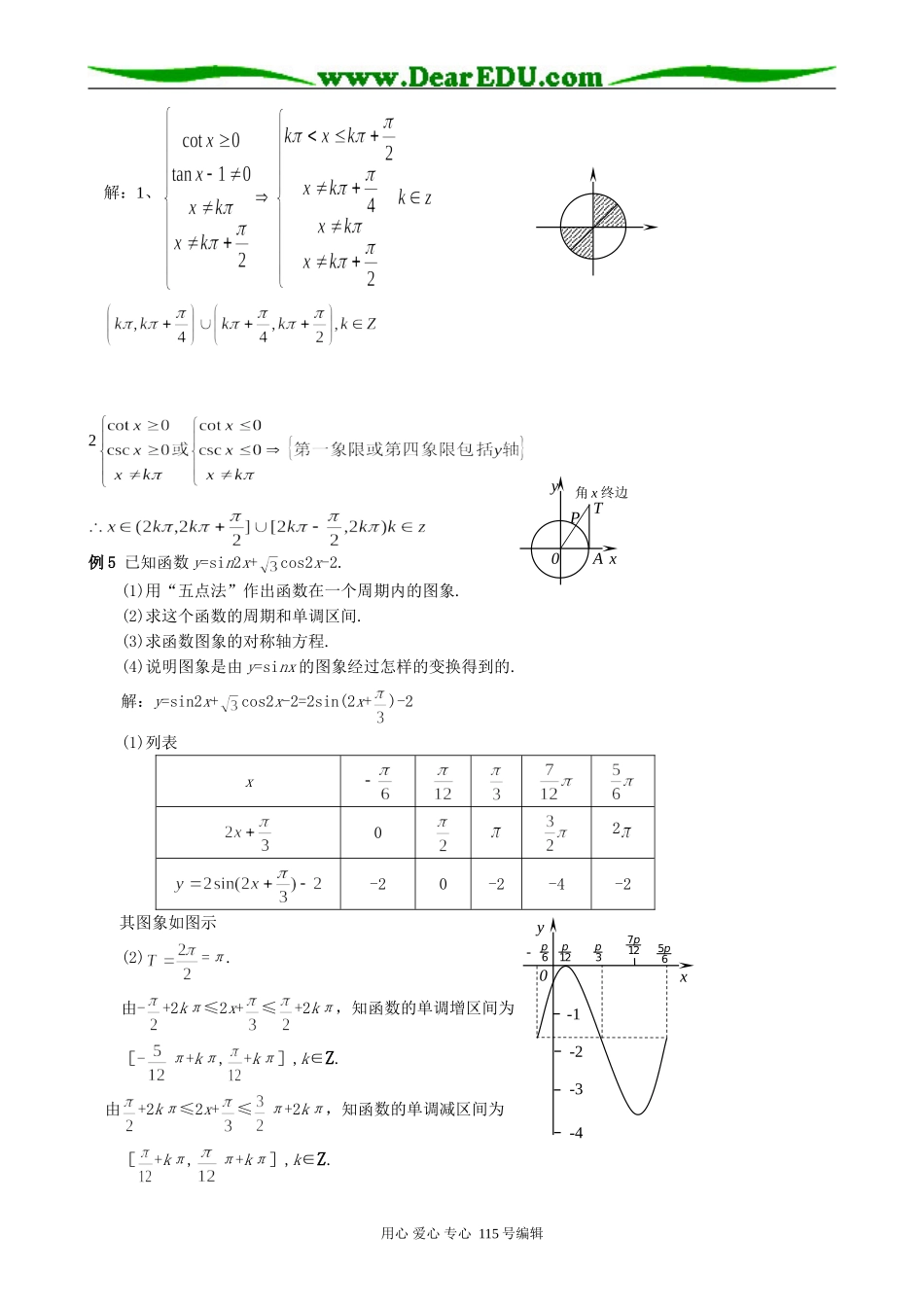
正切函数的图象和性质(2)教学目的:1.掌握正切函数的性质;2.掌握性质的简单应用;3.会解决一些实际问题.教学重点:正切函数的性质的应用.教学难点:灵活应用正切函数的性质解决相关问题.教学过程:一、复习引入:正切线:首先练习正切线,画出下列各角的正切线:正切线是AT.正切函数,且的图象,称“正切曲线”余切函数y=cotx,x∈(kπ,kπ+π),k∈Z的图象(余切曲线)正切函数的性质:1.定义域:,2.值域:R3.当时,当时4.周期性:5.奇偶性:奇函数6.单调性:在开区间内,函数单调递增.余切函数y=cotx,x∈(kπ,kπ+π),k∈Z的性质:1.定义域:用心爱心专心115号编辑xyATα的终边0xyATα的终边0xyATα的终边0xyATα的终边02p-2pxy032p32p-p-p2.值域:R,3.当时,当时4.周期:5.奇偶性:奇函数6.单调性:在区间上函数单调递减.二、讲解范例:例1用图象解不等式解:利用图象知,所求解为亦可利用单位圆求解.例2求函数的定义域、值域,并指出它的周期性、奇偶性、单调性.解:由得,所求定义域为值域为R,周期,是非奇非偶函数.在区间上是增函数.例3作出函数且的简图.解:例4求下列函数的定义域1、2、用心爱心专心115号编辑xyAT03p2p10yx解:1、2例5已知函数y=sin2x+cos2x-2.(1)用“五点法”作出函数在一个周期内的图象.(2)求这个函数的周期和单调区间.(3)求函数图象的对称轴方程.(4)说明图象是由y=sinx的图象经过怎样的变换得到的.解:y=sin2x+cos2x-2=2sin(2x+)-2(1)列表x02-20-2-4-2其图象如图示(2)=π.由-+2kπ≤2x+≤+2kπ,知函数的单调增区间为[-π+kπ,+kπ],k∈Z.由+2kπ≤2x+≤π+2kπ,知函数的单调减区间为[+kπ,π+kπ],k∈Z.用心爱心专心115号编辑xyAT0角x终边P-1-2-3-46p-12p3p712p56pxy0(3)由2x+=+kπ得x=+π.∴函数图象的对称轴方程为x=+π,(k∈Z).(4)把函数y1=sinx的图象上所有点向左平移个单位,得到函数y2=sin(x+)的图象;再把y2图象上各点的横坐标缩短到原来的倍(纵坐标不变),得到y3=sin(2x+)的图象;再把y3图象上各点的纵坐标伸长到原来的2倍(横坐标不变),得到y4=2sin(2x+)的图象;最后把y4图象上所有点向下平移2个单位,得到函数y=2sin(2x+)-2的图象.评注:(1)求函数的周期、单调区间、最值等问题,一般都要化成一个角的三角函数形式.(2)对于函数y=Asin(ωx+φ)的对称轴,实际上就是使函数y取得最大值或最小值时的x值.(3)第(4)问的变换方法不惟一,但必须特别注意平移变换与伸缩变换的先后顺序!例6如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B.(1)求这段时间的最大温差;(2)写出这段曲线的函数解析式.解:(1)由图可知,这段时间的最大温差是30-10=20(℃)(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+B的半个周期的图象.∴·=14-6ω=.又由图可得∴y=10sin(x+φ)+20.将x=6,y=10代入上式得:sin(π+φ)=-1∴故所求的解析式为y=10sin(x+π)+20,x∈[6,14].评注:①本题以应用题的形式考查热点题型,设计新颖别致,匠心独具.②此类“由已知条件或图象求函数的解析式”的题目,实质上是用“待定系数法”确定A,ω,φ和B,它们的计算方法为:ω与周期有关,可通过T=求得,而关键一步在于如何确定φ?通常是将图象上已知点的坐标代入函数解析式,得到一个关于φ的简单三角方程,但φ到底取何值值得考虑.若得方程sinφ=,那么φ是用心爱心专心115号编辑681012141020300xy时间/h温度/0C取,还是取π呢?这就要看所代入的点是在上升的曲线上,还是在下降的曲线上,若在上升的曲线上,φ就取,否则就取π,而不能同时取两个值.例7a为何值时,方程sin2x+2sinxcosx-2cos2x=a有实数解.分析:所给方程的特征较明显,即是关于sinx与cosx的奇式方程,通过变形就可化为以tanx为变元的一元二次方程,从而据判别式进行求解.解法一:原方程可化为:sin2x+2sinxcosx-2cos2x=a(sin2x+cos2x)即(1-a)sin2x+2sinxcosx-(2+a)cos2x=0.(1)当a≠1时, cosx≠0,∴方程两边同除以cos2x得(1-a)tan2x+2tanx-(2+a)=0. tanx∈R∴Δ≥0.即4+4(1-a)(2+a)≥0.即a2+a-3≤0.又a≠1,∴a∈[,1]∪(1,](2)当a=1时,原方程化为2sinxcosx-3cos2x=0,...