高中第一册(下)数学已知三角函数值求角(2)(1)VIP免费

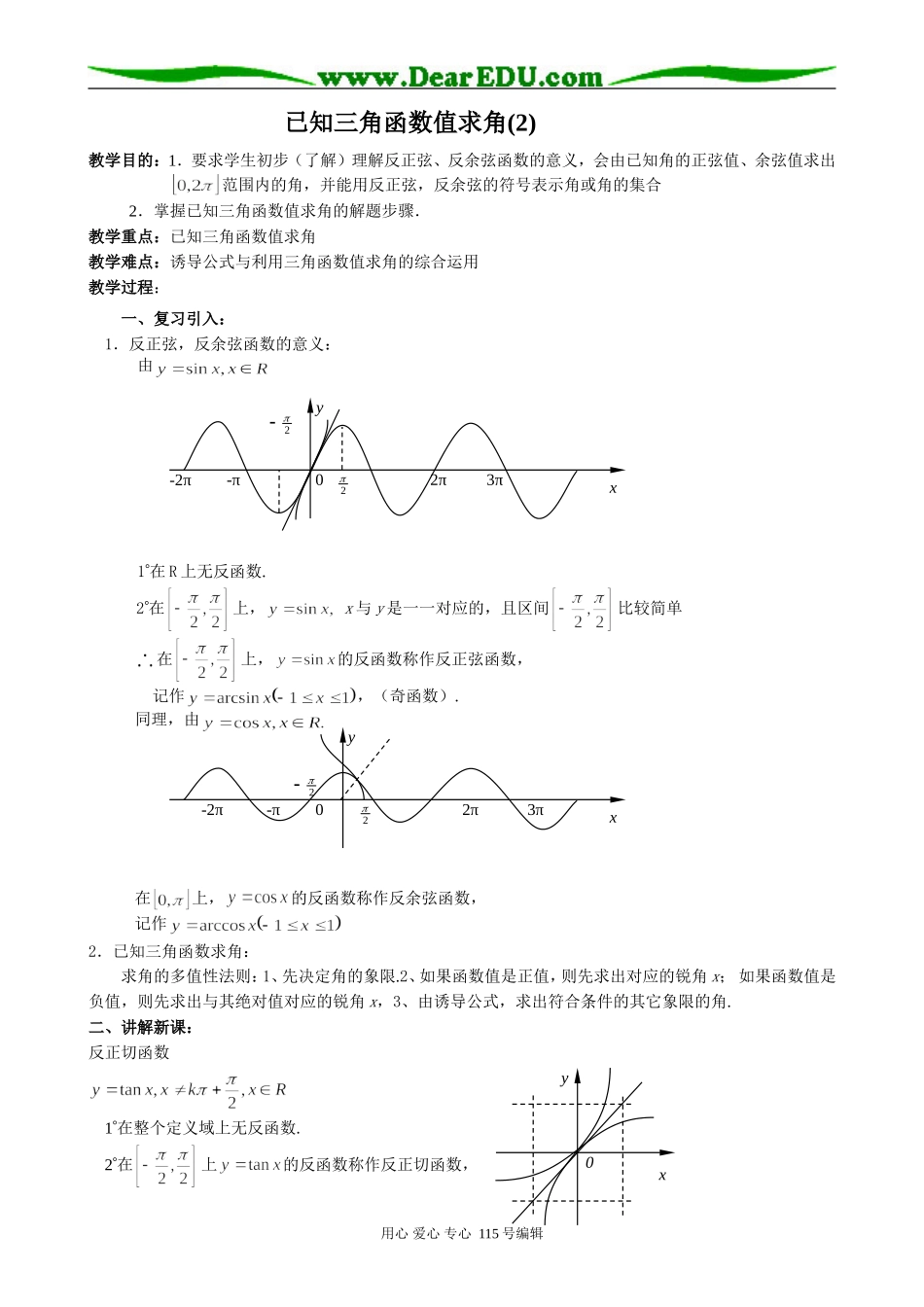
已知三角函数值求角(2)教学目的：1．要求学生初步（了解）理解反正弦、反余弦函数的意义，会由已知角的正弦值、余弦值求出范围内的角，并能用反正弦，反余弦的符号表示角或角的集合2．掌握已知三角函数值求角的解题步骤．教学重点：已知三角函数值求角教学难点：诱导公式与利用三角函数值求角的综合运用教学过程：一、复习引入：1．反正弦，反余弦函数的意义：由1在R上无反函数.2在上，x与y是一一对应的，且区间比较简单在上，的反函数称作反正弦函数，记作，（奇函数）.同理，由在上，的反函数称作反余弦函数，记作2．已知三角函数求角：求角的多值性法则：1、先决定角的象限.2、如果函数值是正值，则先求出对应的锐角x；如果函数值是负值，则先求出与其绝对值对应的锐角x，3、由诱导公式，求出符合条件的其它象限的角.二、讲解新课：反正切函数1在整个定义域上无反函数.2在上的反函数称作反正切函数，用心爱心专心115号编辑2π3π-π-2π220xy2π3π-π-2π220xyxy0记作（奇函数）.三、讲解范例：例1（1）已知，求x（精确到）.解：在区间上是增函数，符合条件的角是唯一的（2）已知且，求x的取值集合.解：所求的x的集合是（即）（3）已知，求x的取值集合.解：由上题可知：，合并为例2已知，根据所给范围求：1为锐角2为某三角形内角3为第二象限角4解：1由题设2设，或34由题设例3求适合下列关系的x的集合.123解：1所求集合为2所求集合为3例4直角锐角A，B满足：用心爱心专心115号编辑解：由已知：为锐角，例51用反三角函数表示中的角x2用反三角函数表示中的角x解：1∵∴又由得∴∴2∵∴又由得∴∴例6已知，求角x的集合.解：∵∴由得由得故角x的集合为例7求的值.解：arctan2=,arctan3=则tan=2，tan=3且，∴而∴+=又arctan1=∴=例8求y=arccos(sinx),()的值域解：设u=sinx∵∴∴∴所求函数的值域为用心爱心专心115号编辑四、课堂练习：1.若cosx＝0，则角x等于()A．ｋπ，（ｋ∈Z）Ｂ．＋ｋπ，（ｋ∈Z）Ｃ．＋2ｋπ，（ｋ∈Z）Ｄ．－＋2ｋπ，（ｋ∈Z）2.若tanx＝0，则角x等于()A．ｋπ，（ｋ∈Z）Ｂ．＋ｋπ，（ｋ∈Z）Ｃ．＋2ｋπ，（ｋ∈Z）Ｄ．－＋2ｋπ，（ｋ∈Z）3.已知cosx＝－，π＜x＜2π，则x等于()A．Ｂ．Ｃ．Ｄ．4.若tan（3π－x）＝－，则x=.5.满足tanx＝的x的集合为.6.在闭区间［0，2π］上，适合关系式cosx＝－0．4099的角有个,用0．4099的反余弦表示的x值是_______；用－0.4099的反余弦表示的x的值是_________.参考答案：1.B2.A3.A4.x＝＋kπ，k∈Z5.｛x｜x＝arctaｎ＋kπ，k∈Z｝6.两π－arccos0.4099π＋arccos0.4099arccos(－0.4099)2π－arccos(－0.4099)五、小结：反正切函数的有关概念，并能运用知识已知三角函数值求角.六、课后作业：1.程cosx＝a（｜a｜＜1，x∈［0，2π的解的集合是()A．｛arccosa，－arccosa｝Ｂ．｛arccosa｝Ｃ．｛arccosa，π－arccosa｝Ｄ．｛arccosa，2π－arccosa｝2.合cosx＝－，x∈（－π，－）的x值是()A．arccos（－）Ｂ．π－arccosＣ．－arccos（－）Ｄ．－arccos3.tanα＝8，且α∈（，），则α等于()A．arctan8Ｂ．arctan8－πＣ．π－arctan8Ｄ．π＋arctan84.3tan2x＝1，x是第三象限角，则x的集合是.5.若tanθ＝8.8，且tan83°31′＝8.8，则θ的集合为.6.若cos2x＝－且0＜x＜2π，则x等于.用心爱心专心115号编辑7.求满足sinxcosx－sinx－cosx－1＝0的x.8.已知sinx＋cosx＝1，求．9.求满足cos（πsinx）＝的x的集合.参考答案：1.D2.C3.D4.x＝＋2kπ，k∈Z5.｛θ｜θ＝83°31′＋k·180°，k∈Z｝6.7.x＝－＋2kπ或x＝π＋2kπ，k∈Z8.19.｛x｜x＝±arcsin＋kπ，k∈Z｝用心爱心专心115号编辑