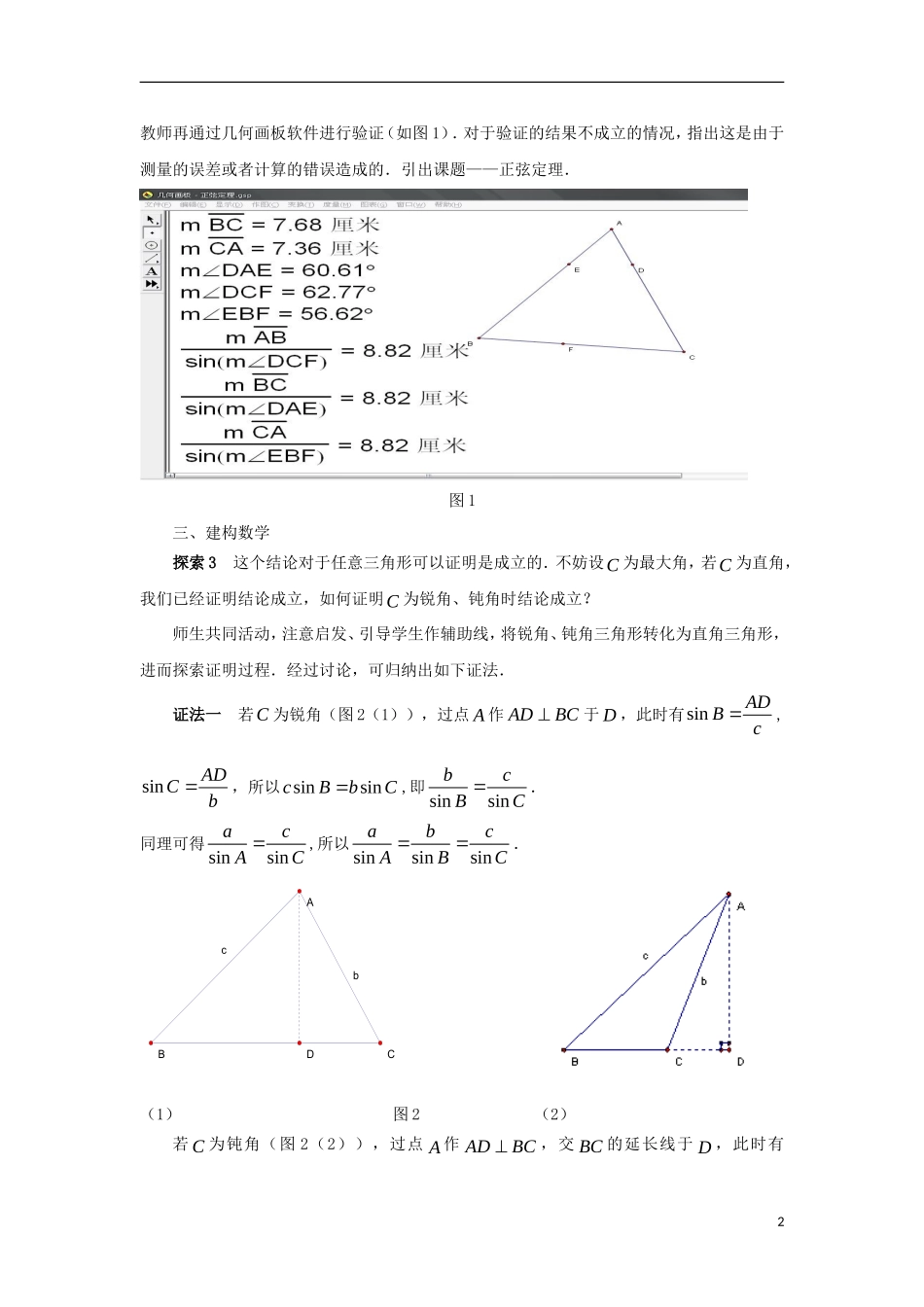
1.1正弦定理教学目标:1.掌握正弦定理及其证明,能够运用正弦定理解决一些简单的三角形度量问题;2.通过对任意三角形的边长和角度关系的探索,培养学生的自主学习和自主探索能力;3.提供适当的问题情境,激发学生的学习热情,培养学生学习数学的兴趣.教学重点:正弦定理及其证明过程.教学难点:正弦定理的推导和证明.教学过程:一、问题情境从金字塔的建造到尼罗河两岸的土地丈量,从大禹治水到都江堰的修建,从天文观测到精密仪器的制造,人们都离不开对几何图形的测量、设计和计算.测量河流两岸两码头之间的距离,确定待建隧道的长度,确定卫星的角度与高度等等,所有这些问题,都可以转化为求三角形的边或角的问题,这就需要我们进一步探索三角形中的边角关系.探索1我们前面学习过直角三角形中的边角关系,在RtABC中,设90C,那么边角之间有哪些关系?sinaAc,sinbBc,sin1cCc,cosbAc,cosaBc,cos0C,tanaAb,sincosAB,sincosBA,1tantanAB……探索2在RtABC中,我们得到sinsinsinabcABC,对于任意三角形,这个结论还成立吗?二、学生活动把学生分成两组,一组验证结论对于锐角三角形是否成立,另一组验证结论对于钝角三角形是否成立.学生通过画三角形、测量长度及角度,再进行计算,得出结论成立.1教师再通过几何画板软件进行验证(如图1).对于验证的结果不成立的情况,指出这是由于测量的误差或者计算的错误造成的.引出课题——正弦定理.图1三、建构数学探索3这个结论对于任意三角形可以证明是成立的.不妨设C为最大角,若C为直角,我们已经证明结论成立,如何证明C为锐角、钝角时结论成立?师生共同活动,注意启发、引导学生作辅助线,将锐角、钝角三角形转化为直角三角形,进而探索证明过程.经过讨论,可归纳出如下证法.证法一若C为锐角(图2(1)),过点A作ADBC于D,此时有sinADBc,sinADCb,所以sinsincBbC,即sinsinbcBC.同理可得sinsinacAC,所以sinsinsinabcABC.cbDABC(1)图2(2)若C为钝角(图2(2)),过点A作ADBC,交BC的延长线于D,此时有2sinADBc,且sinADCb,同理可得sinsinsinabcABC.综上可得,结论成立.证法二利用三角形的面积转化,先作出三边上的高AD、BE、CF,则sinADcB,sinBEaC,sinCFbA.所以ABCS1bcsinA2=1sin2acB=1bcsinA2,每项同时除以12abc,得sinsinsinabcABC探索4充分挖掘三角形中的等量关系,可以探索出不同的证明方法,我们知道向量也是解决问题的重要工具,因此能否从向量的角度来证明这个结论呢?在ABC中,有BCBAAC�,设C为最大角,过点A作ADBC于D,(图3),于是BCADBAADACAD�,设AD�与AC�的夹角为,则0BAAD�cos(90+B)+cosACAD�,其中,当C为锐角或者直角时,90C;当C为钝角时,90C.故可得sinsincBbC0,即sinsinbcBC.同理可得sinsinacAC.因此sinsinsinabcABC.这里运用向量的数量积将向量等式转化为数量等式,我们运用不同的方法证明了三角形中的一个重要定理.探索5这个式子中包含哪几个式子?每个式子中有几个量?它可以解决斜三角型中的哪些类型的问题?3三个式子:sinsinabAB,sinsinbcBC,sinsinacAC.每个式子中都有四个量,如果已知其中三个可求出第四个.正弦定理可以解决两类三角形问题:(1)已知两角与任一边,求其他两边和一角(两角夹一边需要先用三角形内角和定理求出第三角,再使用正弦定理);(2)已知两边和其中一边的对角,求另一边的对角(从而进一步求出其他的边和角).四、数学运用例题在ABC中:(1)已知16a,26b,30A,求B,C,c;(2)已知30a,26b,30A,求B,C,c;(3)已知25a,11b,30B,解这个三角形.解(1)由正弦定理得sinsinabAB,即1626sin30sinB,因此26sin3013sin1616B所以154.3B,或218054.3125.7B.由于2125.730155.7180BA故2B也符合要求,从而本题有两个解154.3B或2125.7B.①当154.3B时,11180()180(54.330)95.7CAB...