高中数学 3.2《一元二次不等式（1）》教案（苏教版必修5）VIP免费

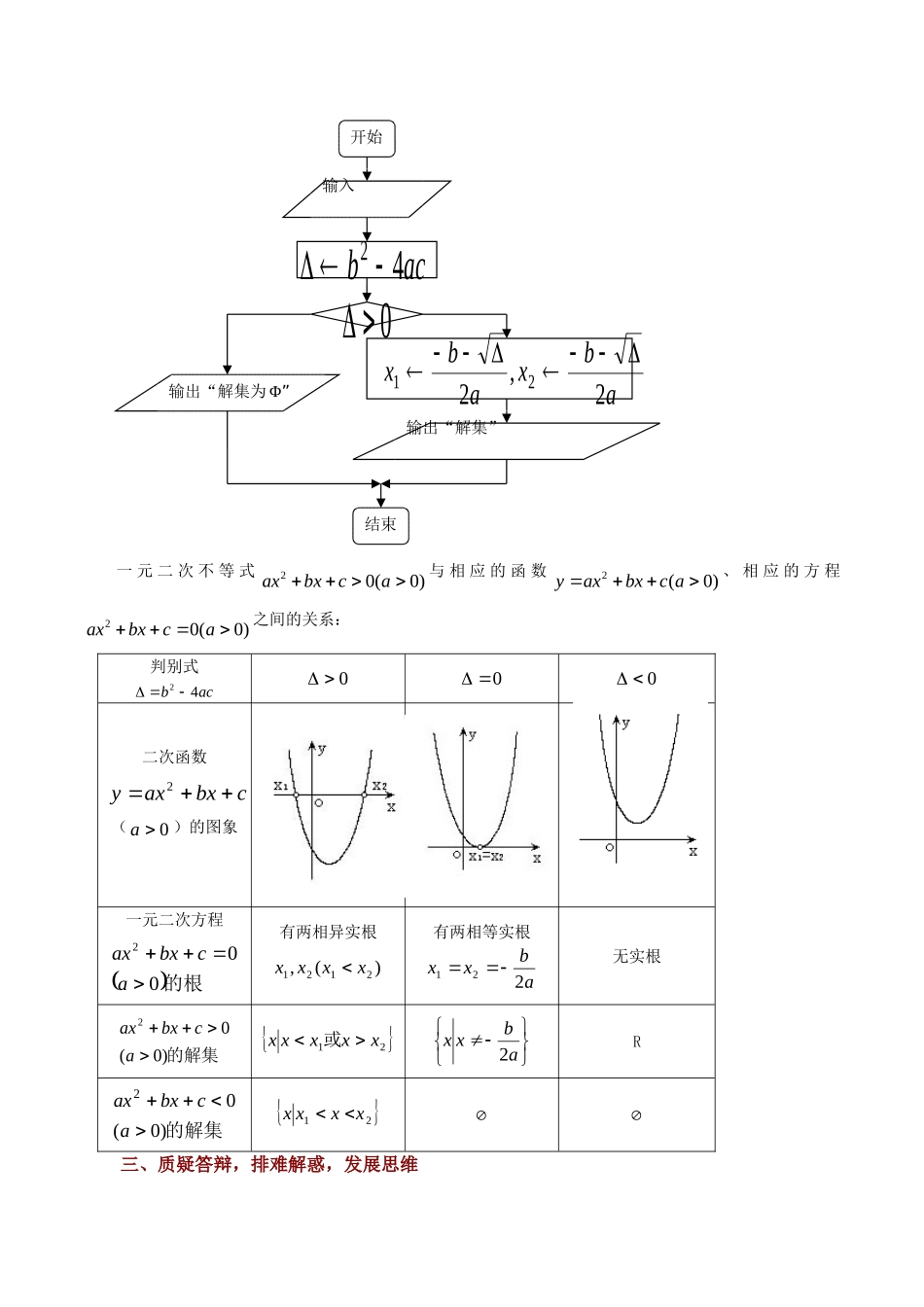
第2课时：§3.2一元二次不等式（1）【三维目标】：一、知识与技能1.通过函数图像了解一元二次不等式与相应函数、方程的联系；2.会解一元二次不等式，对给定的一元二次不等式，尝试设计求解的程序框图；3.掌握利用因式分解和讨论来求解一元二次不等式的方法及这种方法的推广运用；4.培养数形结合、分类讨论、等价转化的思想方法，培养抽象概括能力和逻辑思维能力；通过看图象找解集，培养学生从“从形到数”的转化力，“由具体到抽象”、“从特殊到一般”的归纳概括能力。二、过程与方法经历从实际情境中抽象出一元二次不等式模型的过程和通过函数图象探究一元二次不等式与相应函数、方程的联系，获得一元二次不等式的解法；三、情感、态度与价值观1.激发学生学习数学的热情，培养勇于探索的精神，培养学生的合作意识和创新精神，同时体会事物之间普遍联系的辩证思想；通过等与不等的对立统一关系的认识，对学生进行辨证唯物主义教育.2.创设问题情景，激发学生观察、分析、探求的学习激情、强化学生参与意识及主体作用。【教学重点与难点】：重点：从实际情境中抽象出一元二次不等式模型；一元二次不等式的解法。难点：理解二次函数、一元二次方程与一元二次不等式解集的关系。【学法与教学用具】：1.学法：2.教学方法：诱思引探教学法3.教学用具：多媒体、实物投影仪.【授课类型】：新授课【课时安排】：1课时【教学思路】：一、创设情景，揭示课题观察函数25104.8yxx的图象，可以看出，一元二次不等式25104.80xx的解集就是二次函数25104.8yxx的图象（抛物线）位于x轴下方的点所对应的x值的集合．因此，求解一元二次不等式可以先解相应的一元二次方程，确定抛物线与x轴交点的横坐标，再根据图象写出不等式的解集．第一步：解方程25104.80xx，得120.8,1.2xx；第二步：画出抛物线25104.8yxx的草图；第三步：根据抛物线的图象，可知25104.80xx的解集为{|0.81.2}xx．二、研探新知求解一元二次不等式20(0)axbxca的过程，可用下图所示和流程图来描述：一元二次不等式20(0)axbxca与相应的函数2(0)yaxbxca、相应的方程20(0)axbxca之间的关系：判别式acb42000二次函数cbxaxy2（0a）的图象一元二次方程的根002acbxax有两相异实根)(,2121xxxx有两相等实根abxx221无实根的解集)0(02acbxax21xxxxx或abxx2R的解集)0(02acbxax21xxxx三、质疑答辩，排难解惑，发展思维开始输入acb420abxabx2,221输出“解集”输出“解集为Φ”结束例1解下列不等式：（1）27120xx；（2）2230xx；（3）2210xx；（4）2220xx．解：（1）方程27120xx的解为123,4xx．根据2712yxx的图象，可得原不等式27120xx的解集是{|34}xxx或．（2）不等式两边同乘以1，原不等式可化为2230xx．方程2230xx的解为123,1xx．根据223yxx的图象，可得原不等式2230xx的解集是{|31}xx．（3）方程2210xx有两个相同的解121xx．根据221yxx的图象，可得原不等式2210xx的解集为．（4）因为0，所以方程2220xx无实数解，根据222yxx的图象，可得原不等式2220xx的解集为．思考：（1）求解一元二次不等式20(0)axbxca的过程，怎样用流程图来描述？（2）求解一元二次不等式20(0)axbxca的过程，怎样用流程图来描述？（3）不等式20(0)axbxca和20(0)axbxca的解法？结论：1.一元二次不等式的解集：（1）不等式)0(0))((21axxxxa的解集为}|{21xxxx（2）不等式)0(0))((21axxxxa的解集为1|{xxx或}2xx（其中21xx）2.归纳解一元二次不等式的步骤：（1）二次项系数化为正数；（2）解对应的一元二次方程；（3）根据一元二次方程的根，结合不等号的方向画图；（4）写出不等式的解集．即：一化正→二算Δ→三求根→四写解集例2已知关于x的不等式20...