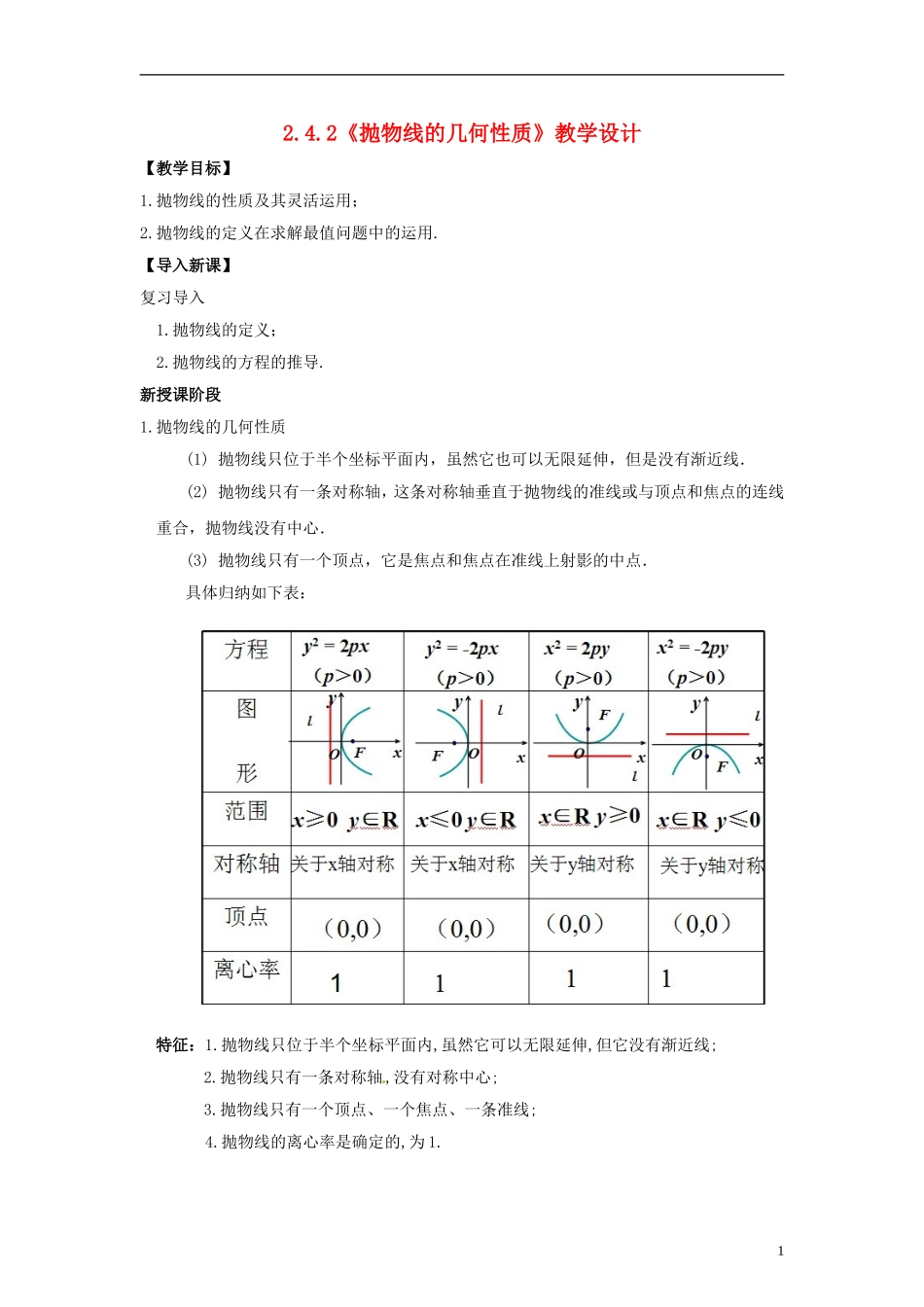
2.4.2《抛物线的几何性质》教学设计【教学目标】1.抛物线的性质及其灵活运用;2.抛物线的定义在求解最值问题中的运用.【导入新课】复习导入1.抛物线的定义;2.抛物线的方程的推导.新授课阶段1.抛物线的几何性质(1)抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但是没有渐近线.(2)抛物线只有一条对称轴,这条对称轴垂直于抛物线的准线或与顶点和焦点的连线重合,抛物线没有中心.(3)抛物线只有一个顶点,它是焦点和焦点在准线上射影的中点.具体归纳如下表:特征:1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的,为1.1例1.已知抛物线关于x轴对称,顶点在坐标原点,并且过点M(2,),求它的标准方程.例2斜率为1的直线经过抛物线的焦点,且与抛物线相交于A,B两点,求线段的长.解:抛物线的焦点F(1,0),课堂小结(一)本节课我们学习了抛物线的几个简单几何性质:范围、对称性、顶点坐标、离心率等概念及其几何意义.(二)了解了研究抛物线的焦半径,焦点弦和通径这对我们解决抛物线中的相关问题有很大的帮助.(三)在对曲线的问题的处理过程中,我们更多的是从方程的角度来挖掘题目中的条件,认识并熟练掌握数与形的联系.在本节课中,我们运用了数形结合,待定系数法来求解抛物线方程,在解题过程中,准确体现了函数与方程以及分类讨论的数学思想.作业见同步练习部分拓展提升21.抛物线上的一点到焦点的距离为1,则点的纵坐标是()A.B.C.D.02.已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,满足|MN|·|MP|+MN·NP=0,则动点P(x,y)的轨迹方程是()A.y2=8xB.y2=-8xC.y2=4xD.y2=-4x3.已知P是抛物线y=2x2+1上的动点,定点A(0,―1),点M分PA所成的比为2,则点M的轨迹方程是()A.y=6x2―B.x=6y2-C.y=3x2+D.y=―3x2―14.有一个正三角形的两个顶点在抛物线y2=2x上,另一个顶点在原点,则这个三角形的边长是.5.对正整数,设抛物线,过任作直线交抛物线于两点,则数列的前项和公式是.6.焦点在x轴上的抛物线被直线y=2x+1截得的弦长为,求抛物线的标准方程.7.定长为3的线段AB的两个端点在抛物线y2=x上移动,AB的中点为M,求点M到y轴的最短距离,并求出点M的坐标.38.在直角坐标系中,已知点(p>0),设点F关于原点的对称点为B,以线段FA为直径的圆与y轴相切.⑴点A的轨迹C的方程;⑵PQ为过F点且平行于y轴的曲线C的弦,试判断PB与QB与曲线C的位置关系.是曲线C的平行于y轴的任意一条弦,若直线FM1与BM2的交点为M,试证明点M在曲线C上.4参考答案1.B【解析】用抛物线的定义.2.B【解析】坐标代入.3.B【解析】用坐标转移法.4.12【解析】有两个顶点关于x轴对称,进而得到直线的倾斜角是和.5.【解析】求出数列的通项公式.6.y2=12x或y2=-4x【解析】设抛物线方程后,用韦达定理及弦长公式.7.M()或()【解析】数形结合得到当且仅当AB过焦点时M到y轴距离最小.设出此时的直线方程,用弦长公式解得直线AB的斜率,并得到AB的坐标.8.解:(1)设A(x,y),则,化简得:y2=2px(2)由对称性知,PB和QB与曲线C的位置关系是一致的,由题设,不妨P()而∴直线PB的方程为y=x+,代入y2=2px,消去y得到关于x的一元二次方程x2+px+=0,=0∴直线PB和QB均与抛物线相切.(3)由题意设,,则直线FM1:;直线BM2:联立方程组解得M点坐标为,,经检验,,∴点M在曲线C上.5