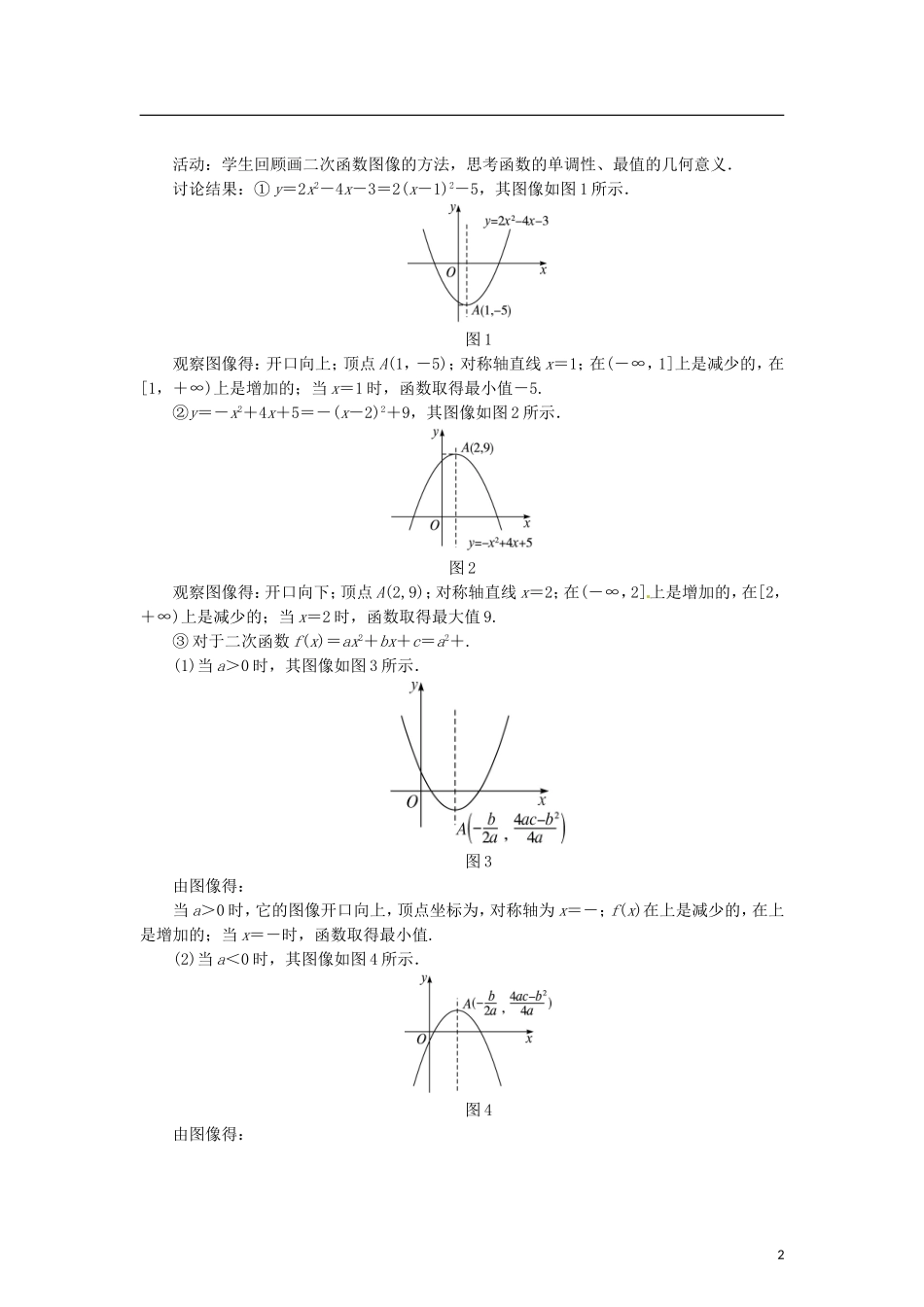
4.2二次函数的性质\s\up7()教学分析在讨论二次函数性质的过程中,其图像显然起了重要作用,但是又不忽视解析式的作用.因此教材突出数与形的有机结合.本节教材先给出了抽象的字母形式的配方结果,进而从字母出发对a>0时函数的单调性进行了证明.与二次函数的图像一节相比,例题也比较综合,有一定的难度.可以而且应该适度综合,适度抽象.高中学生,已经处于思维接近成熟的阶段,有些情况下,不能就事论事,而应该适度思考一些带有综合性的问题,但不可过分.对一般学生来说,分寸掌握到课本例题和习题的水平为宜.程度好一些的学生,当然,也可以自选一些题目来做.对于抽象的一般二次函数单调性证明,用文字表示对称轴、顶点、最大(小)值、单调区间等,教师应该带领学生尝试.解决实际问题,是数学学习的重要目的,也是引起学生思考的重要方法.有些例题,如例3,意在联系实际.但是,编者眼界有限.教师,可以而且应该具有这种意识,自己出马或发动学生根据当地实际再编写一些联系实际的问题.值得注意的是课上注意组织学生动手,活动,实践.教材中安排了学生的“动手实践”和“思考交流”.教师,要创造性地用好它们.三维目标对一般二次函数解析式配方,确定其位置,并能研究其定义域、值域、单调性、最大(小)值等性质,提高学生数形结合的能力.重点难点教学重点:二次函数的性质.教学难点:应用二次函数的性质解决实际问题.课时安排1课时\s\up7()导入新课思路1.上一节课,我们学习了二次函数的图像,本节课我们来学习二次函数的性质.思路2.“菊花”烟花是最壮观的烟花之一,人们在制造时一般是期望在它达到最高点(大约是距地面25米到30米处)时爆炸,烟花冲出去后的运动路线是抛物线形的,为了达到放烟花的最佳效果,烟花设计者按照有关的数据设定引线的长度,如果是你来设计,你可以吗?教师引出课题.推进新课①画出y=2x2-4x-3的图像,根据图像讨论图像的开口方向、顶点坐标、对称轴、单调区间、最大值和最小值.②画出y=-x2+4x+5的图像,根据图像讨论图像的开口方向、顶点坐标、对称轴、单调区间、最大值和最小值.③讨论二次函数fx=ax2+bx+ca≠0图像的开口方向、顶点坐标、对称轴、单调区间、最大值和最小值.1活动:学生回顾画二次函数图像的方法,思考函数的单调性、最值的几何意义.讨论结果:①y=2x2-4x-3=2(x-1)2-5,其图像如图1所示.图1观察图像得:开口向上;顶点A(1,-5);对称轴直线x=1;在(-∞,1]上是减少的,在[1,+∞)上是增加的;当x=1时,函数取得最小值-5.②y=-x2+4x+5=-(x-2)2+9,其图像如图2所示.图2观察图像得:开口向下;顶点A(2,9);对称轴直线x=2;在(-∞,2]上是增加的,在[2,+∞)上是减少的;当x=2时,函数取得最大值9.③对于二次函数f(x)=ax2+bx+c=a2+.(1)当a>0时,其图像如图3所示.图3由图像得:当a>0时,它的图像开口向上,顶点坐标为,对称轴为x=-;f(x)在上是减少的,在上是增加的;当x=-时,函数取得最小值.(2)当a<0时,其图像如图4所示.图4由图像得:2当a<0时,它的图像开口向下,顶点坐标为,对称轴为x=-;f(x)在上是增加的,在上是减少的;当x=-时,函数取得最大值.下面证明当a>0时,函数f(x)在上是减少的,在上是增加的.证明:设a>0,任取x1、x2,且x1<x2≤-,则f(x2)-f(x1)=(ax+bx2+c)-(ax+bx1+c)=a(x-x)+b(x2-x1)=[a(x2+x1)+b](x2-x1).因为x1<-,x2≤-,所以x1+x2<-,即a(x1+x2)<-b.也就是a(x1+x2)+b<0.又x2-x1>0,所以f(x2)-f(x1)<0,即f(x2)<f(x1).由函数单调性的定义,f(x)在上是减少的.同理可证,f(x)在上是增加的.显然,将f(x)=ax2+bx+c配方成f(x)=a2+之后,我们就可以通过a,-和直接得到函数的主要性质,并且可以依此画出函数图像.思路1例1将函数y=-3x2-6x+1配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值,并画出它的图像.活动:学生回顾思考如何由二次函数的解析式讨论其性质.解:y=-3x2-6x+1=-3(x+1)2+4.由于x2的系数是负数,所以函数图像开口向下;图5顶点坐标...