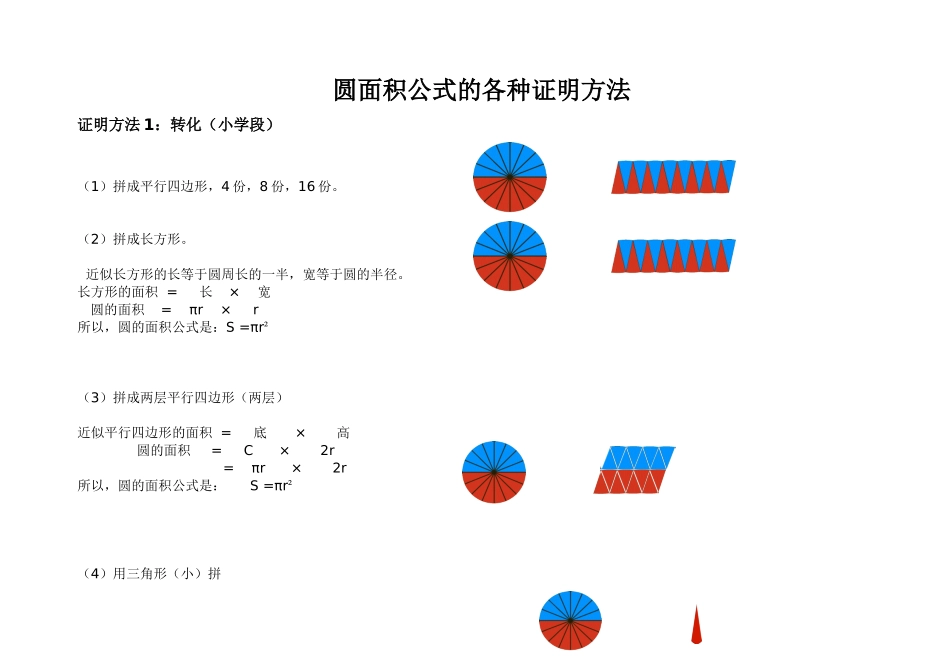
圆面积公式的各种证明方法证明方法1:转化(小学段)(1)拼成平行四边形,4份,8份,16份。(2)拼成长方形。近似长方形的长等于圆周长的一半,宽等于圆的半径。长方形的面积=长×宽圆的面积=πr×r所以,圆的面积公式是:S=πr²(3)拼成两层平行四边形(两层)近似平行四边形的面积=底×高圆的面积=C×2r=πr×2r所以,圆的面积公式是:S=πr²(4)用三角形(小)拼三角形的面积=×底×高圆的面积=×(×C)×r×16所以,圆的面积公式是:S=πr²(5)拼成梯形梯形的面积=(上底+下底)×高圆的面积=×(+)×C×2r所以,圆的面积公式是:S=πr²拼成三角形(大)(6)三角形的面积=底×高圆的面积=×(×C)×4r所以,圆的面积公式是:S=πr²证明方法2:半径为r的圆的圆周长为2πr1.先将圆周等分成n份:每份长为2πr/n.2.连接每个分点与圆心,并且连接各个分点,组成三角形.3.那么,根据三角形面积公式,该圆的面积近似等于:(n-1)·r·(2πr)/n/2.(因为在n充分大时,各个三角形的高近似等于r,并且有n-1个三角形,所以有该公式)取极限:lim(n→+∞)(n-1)·r·(2πr)/n/2,因为lim(n→+∞)(n-1)/n=1所以lim(n→+∞)(n-1)·r·(2πr)/n/2=πr^2证明方法3:极限法(高中段:以圆的正n边形表示圆的面积:设圆的半径为r,内接一个正n边形,它的任意一边所对的圆心角为2π/n,先算出其中一个三角形的面积(用两边夹角的公式S=(1/2)a*b*sinC),然后得到这个正n六边形的面积:Sn=(n/2)r²sin(2π/n)当n无限增大时,内接正n边形的形状无限接近于圆,它的面积也无限接近圆的面积.求这个极限要用一高等数学中一个重要的极限公式(函数的极限):当x→0时,lim[(sinx)/x]=1[题外话:这个极限的几何意义是,当x无限减小时,y=sinx的图象与直线y=x是重合的,在这种情况下,我们可以用x的值来代替sinx,以在某些领域做近似计算]把Sn变形:Sn=πr²lim[sin(2π/n)/(2π/n)]于是,当n→∞时,2π/n→0lim[sin(2π/n)/(2π/n)]=1Sn=πr²证明方法4:极坐标法设圆的极坐标方程R(θ)=R圆心角为dθ扇形的面积dA=1/2R^2dθ.则圆的面积为A=∫(0-2π)dA=∫(0-2π)1/2R^2dθ=πR^2在极坐标系中,圆心在原点,圆的半径r。取一微小的圆心角dθ,对应的弧长rdθ,由于rdθ极短,可以看成直线,则这个微小的扇形可以看成是一直角三角形,面积ds=(1/2)*r*r*dθ。对ds积分就得到圆面积:S=∫ds=(1/2)∫(r^2)dθ(积分下限为0,上限为2π),所以S=πr^2证明方法5:微积分一个圆可以看成是无数个同心圆环组成,设所求圆的半径为R,任取某一个内径为r,外径为r+dr的同心圆环,由于dr很小,可以认为将圆环沿径向剪开后,展开得到的是一个长为2πr,宽为dr的矩形(近似的),易知其面积为2πrdr。设面积微元dA=2πrdr。A=∫2πrdr(积分下限是0,积分上限是R)=πR^2证明方法6:见下图