第三章 一阶系统的时间响应VIP免费

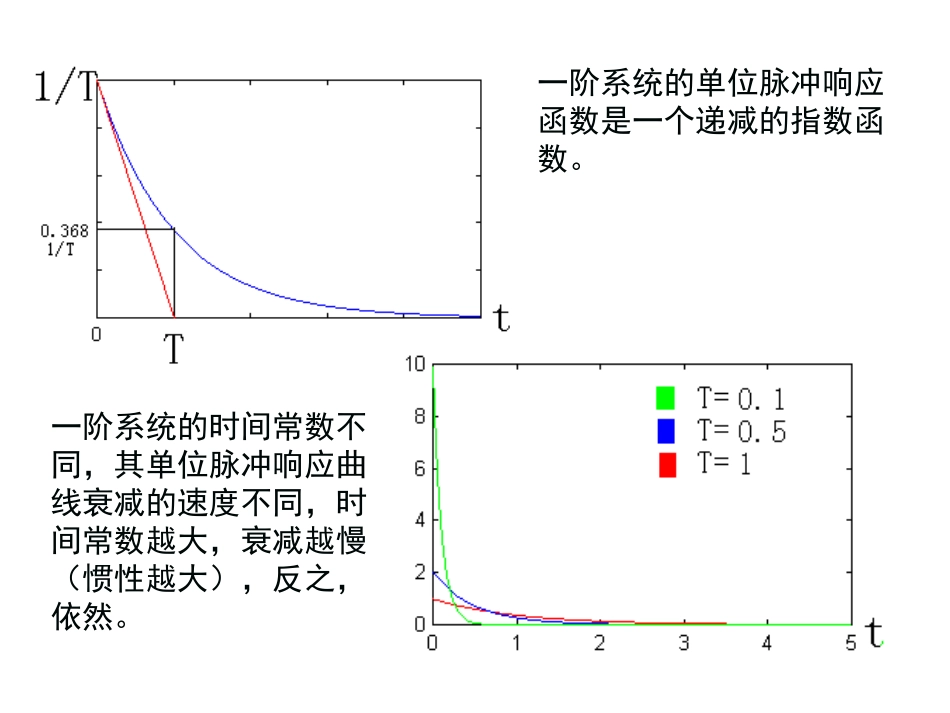
第3节一阶系统的时间响应一、一阶系统可用一阶微分方程表示的系统，称为一阶系统。其微分方程的一般形式为11)()()()()()(TssXsXsGtxtxtxTioioo其中，T称为一阶系统的时间常数，是一阶系统的特征参数。二、一阶系统的单位脉冲响应当系统的输入信号是理想的脉冲函数时，系统的输出称为系统的单位脉冲响应函数（或单位脉冲响应）。)(tw20/20/11111)(.1)(00)()0(1)(]11[)]([)]([)()()().()()(1)()()(TeTtwTtwttwteTtwTsLsGLsWLtwsGsXsGsXsWsXttxtTttTtioii时，只有瞬态项，稳态项为显然，所以，因为系统的输入一阶系统的单位脉冲响应函数是一个递减的指数函数。一阶系统的时间常数不同，其单位脉冲响应曲线衰减的速度不同，时间常数越大，衰减越慢（惯性越大），反之，依然。⊿一般为2%或5%一阶系统过渡过程：•一阶系统的单位脉冲响应曲线从初值衰减到初值的2%或初值的5%所经历的过程。过渡过程时间（调整时间）：•一阶系统的单位脉冲响应曲线从初值衰减到初值的2%或初值的5%所经历的时间。•当⊿取2%时，一阶系统过渡过程时间约为4T。一阶系统的时间常数不同，其调整时间不同，时间常数越大，过渡过程越长（惯性越大），反之，依然。三、一阶系统的单位阶跃响应当系统的输入信号是理想的阶跃函数时，系统的输出称为系统的单位阶跃响应函数（或单位阶跃响应）。)0(1)(]111[]1.11[]1).([)]([)(1).()().()(/1)()()(/1111tetxTssLsTsLssGLsXLtxssGsXsGsXssXtutxTtouoouiouii所以，因为系统的输入TeTtxeTtxtxtetxtetxtTttouTtououTtouTtou11)(1)(.0)(01)()0(1)(0/0///时，，稳态项为瞬态项为显然，一阶系统的单位函数响应函数是一个递增的指数函数。一阶系统的时间常数不同，其单位阶跃响应曲线上升的速度不同，时间常数越大，上升越慢（惯性越大），反之，依然。⊿一般为2%或5%，称为容许误差一阶系统过渡过程：•一阶系统的单位阶跃响应曲线从初值上升到稳态值的98%或稳态值的95%所经历的过程。过渡过程时间（调整时间）：•一阶系统的单位响应曲线从初值上升到稳态值的98%或稳态值的95%所经历的时间。•当⊿取2%时，一阶系统过渡过程时间约为4T。一阶系统的时间常数不同，其调整时间不同，时间常数越大，过渡过程越长（惯性越大），反之，依然。四、系统传递函数与单位脉冲响应函数之间的关系变换对。构成一个数响应函数与系统传递函因此，系统的单位脉冲变换。冲响应函数的系统传递函数是单位脉逆变换；统传递函数的单位脉冲响应函数是系当系统的输入为LaplaceLaplaceLaplacesGLsWLtwsGsXsGsXsWsXttxioii)]([)]([)()()()()()(1)()()(11应用这个结论,在实验建模时,我们只要测到系统的单位脉冲响函数,然后,对其进行Laplace变换就可以求得系统的传递函数.这对于所有的线性定常系统都适用.换言之,单位脉冲响应函数同样反映了系统的动态特性,因此,常常将系统的单位脉冲响应函数也称为系统的数学模型.不过,相对于传递函数或微分方程,它不能直接反映系统的结构(如阶次等)和参数,故称为系统的非参数化数学模型.而将微分方程和传递函数等反映系统的结构和参数这样一类数学模型称为参数化的数学模型.应用这个结论,在实验建模时,我们只要测到系统的单位脉冲响函数,然后,对其进行Laplace变换就可以求得系统的传递函数.这对于所有的线性定常系统都适用.一阶系统对典型输入信号的响应输入信号时域输入信号频域输出响应传递函数11(t)t0tTeTtTt0)1(2122teTTttTt01teTt)0(1teTTt)(tS121S31S221t11TS微分微分等价关系：系统对输入信号导数的响应，就等于系统对该输入信号响应的导数；系统对输入信号积分的响应，就等于系统对该输入信号响应的积分；积分常数由零初始条件确定。第4节二阶系统的时间响应一、二阶系统可用二阶微分方程表示的系统，称为二阶系统。其微分方程的一般形式为222222)()()()()()(2)(nnnioinononosssXsXsGtxtxtxtx特性。二阶系统与外...