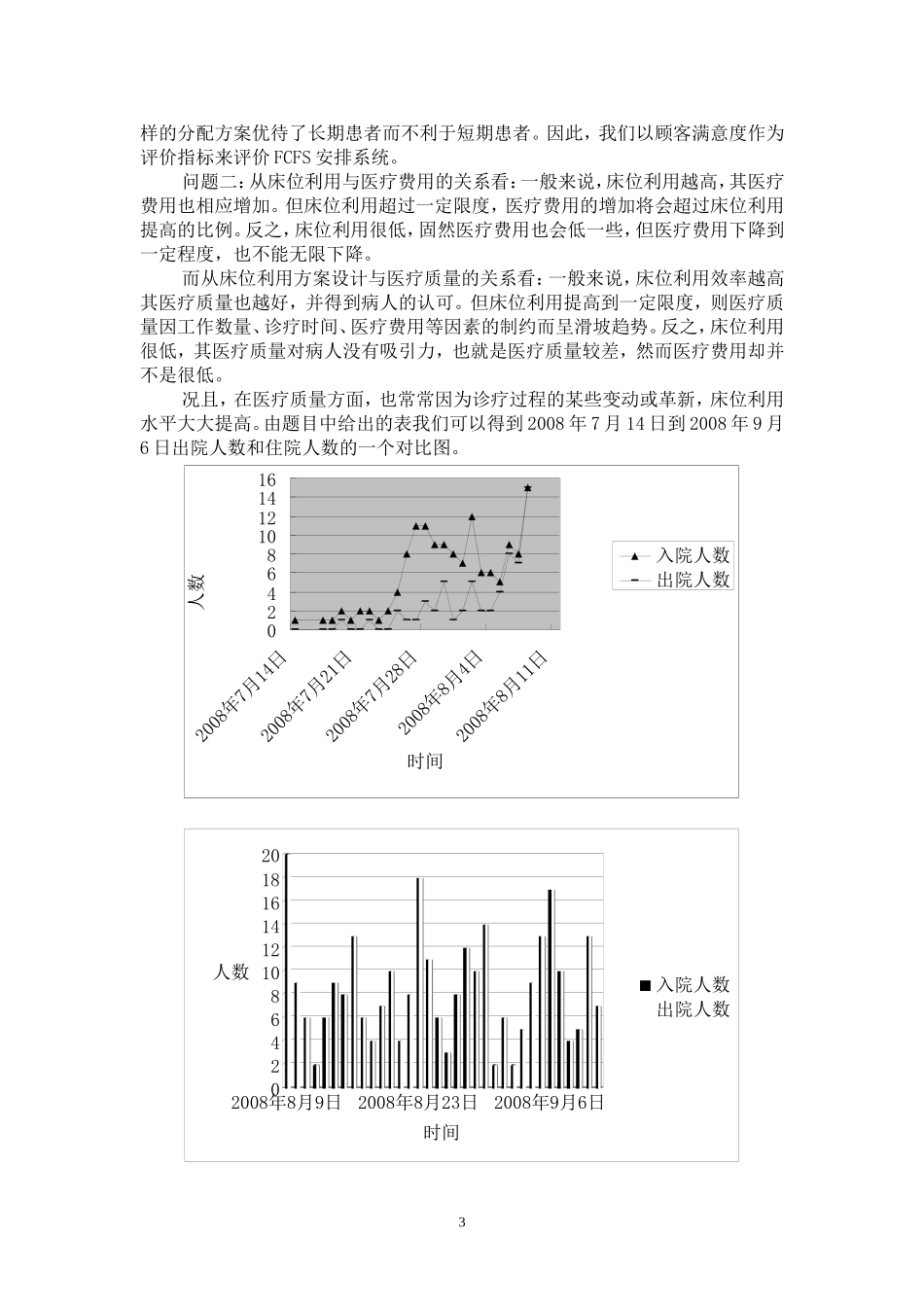
对眼科病床安排模型和评价的探究摘要排队问题在就医领域涉及极为广泛,医院的各个部门都可能存在排队问题,包括临床服务中的门诊、急诊、配药或药材的库存等等。本文以某医院眼科门诊为背景,进而研究、讨论该院部眼科病床的合理安排问题。我们使用归一分析法Markov过程和蒙特卡罗法、计算机模拟仿真等方法对问题进行分析求解,建立了合理的病床安排模型和评价体系。针对问题一:我们将顾客的满意度,作为评价模型的标准之一,结合归一分析法建立效率指数模型(为期内床位实际周转次数,为期内床位标准周转次数,为床位使用率,为效率指数),来判断床位工作效率情况其中,表示第类病人第类等待时间(,),表示第类病人第类等待时间的权重;的值越大说明顾客的满意度越高。针对问题二:我们将病人分为四类,即白内障、视网膜疾病、青光眼、外伤,首先考虑了增加床位的情况,我们建立了Markov模型,找到需要增加床位的最优解,之后我们建立了一个动态优化模型,根据每一类人数的权重确定所需病床数,从而确定最终的病床分配数。最后,我们又运用EDD排队策略对模型进行了进一步讨论,并通过编程模拟确定每天出院人数以及安排住院的人数,并用我们的指标进行了评价,结果显示我们的模型比FCFS模型好。针对问题三:我们以表示第类病人的逗留时间,表示平均每天的出院人数,表示最长住院时间。建立线性模型,模拟出病人的入院区间。针对问题四:根据材料我们就知道了周一和周三只做白内障手术,而且视网膜疾病手术、青光眼手术和白内障手术不排在一天做。现在该住院部在周六和周日不安排手术,那么我们可以认为视网膜疾病手术和青光眼手术只能安排在周二周四、和周五做。而且,由于外伤的随机性,我们约定外伤手术可以在一周内的任何时间做,不受该院部手术安排的限制。针对问题五:首先,我们建立了最优化模型,在此基础上设计了计算机模拟仿真模型。在进行模拟仿真时我们对各类病人在系统的频度进行了分析,用二位随机数来模拟病人服务的情况。通过统计发现每天的外伤人数较少,故我们可用随机数05,45,75来模拟,经过多次使用蒙特卡罗算法模拟,使平均逗留时间达到最短。为实现方便我们只模拟3张病床的情况。在文章的最后,我们还对模型进行了验证与评价,确保了模型的精确性与可靠性。1关键词:效率指数及满意度Markov模型动态优化和EDD排队策略蒙特卡罗法一问题重述现如今,排队就医早就已经成为大家都习以为常的事情了。医院的各个部门都可能存在排队问题,包括临床服务中的门诊、急诊、检验、放射、配药或药材的库存等等。而我们今天要讨论的就是眼科病床的合理安排问题。我们已经知道这家医院眼科门诊每天都开放,接待的患者主要有四种:白内障、视网膜疾病、青光眼和外伤,且该家医院有病床79张。原来医院是按FCFS(Firstcome,Firstserve)规则安排住院,但是等待住院的病人队列越来越长,医院资源的有效利用越来越不好,医院希望用数学建模来帮助解决该住院部的病床合理安排问题,使医院的资源得到最有效的利用。问题一:我们需要确定一个合理的评价指标体系,评价一下该问题中的病床安排模型。问题二:结合实际情况建立一个较为合理的病床安排模型,根据已知的第二天拟出院人数来确定第二天应该安排哪些病人出院,并利用评价指标体系评价这个新建模型。问题三:根据当时住院病人和等待住院病人的统计情况,在病人门诊时告知其大致入住时间。问题四:当该住院部周六、周日不安排手术时,建立一个合理的病床安排模型,并对医院的手术安排时间做出合理的调整。问题五:根据医院病床安排采取各类病人占用的病床的比例大致相同的方案,建立使所有病人在系统内平均逗留时间(含等待入院及住院时间)最短的病床比例分配模型。二问题分析我们主要讨论的是在各种情况下眼科病床的合理安排问题,这里面牵涉到两个不同的个体:服务方(医院)和受服务方(病人)。从病人的角度上,他们关心的是服务的等候时间和接受访问的时间,这直接关系到病人对医院的满意程度;而从医院角度上看,医院更为关心的是为这些顾客完成服务所付出的成本,使用较低的成本又保证病人不至于流失,这是医院决策者...