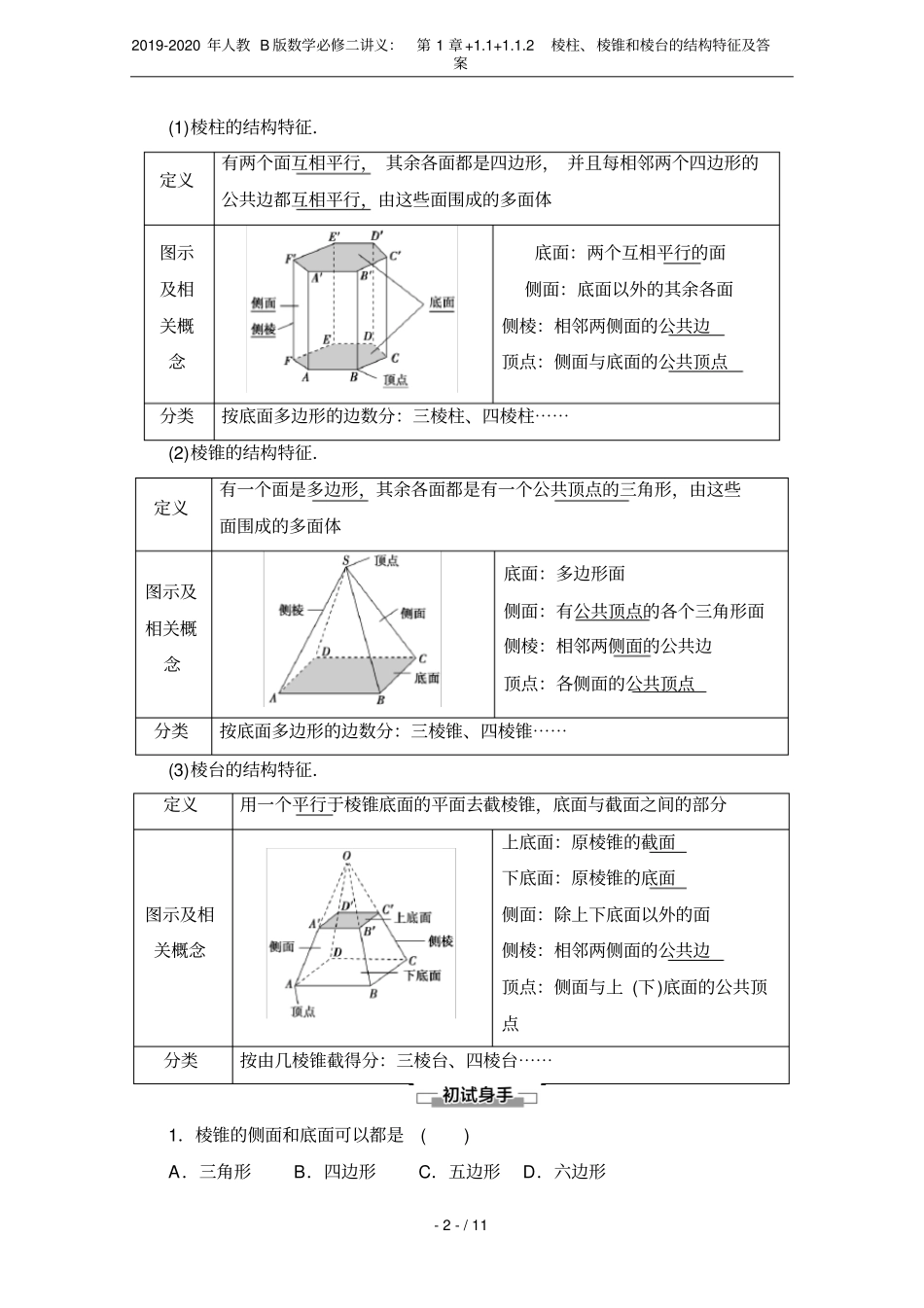
2019-2020年人教B版数学必修二讲义:第1章+1.1+1.1.2棱柱、棱锥和棱台的结构特征及答案-1-/111.1.2棱柱、棱锥和棱台的结构特征学习目标核心素养1.了解多面体的定义及其分类.(重点)2.理解棱柱、棱锥、棱台的定义和结构特征.(重点)3.在棱柱、棱锥、棱台中构造恰当的特征图形,研究其中的线段数量关系和位置关系.(难点)1.通过多面体的定义与分类学习,培养学生的数学抽象核心素养.2.借助棱柱、棱锥、棱台结构特征的学习,培养直观抽象的数学核心素养.1.多面体(1)定义由若干个平面多边形所围成的几何体叫做多面体.(2)相关概念(如图所示)(3)凸多面体把一个多面体的任意一个面延展为平面,如果其余的各面都在这个平面的同一侧,则这样的多面体就叫做凸多面体.思考1:长方体、正方体是多面体吗?[提示]是.长方体是由6个矩形围成的,正方体是由6个正方形围成的,均满足多面体的定义.思考2:最简单的多面体由几个面所围成?[提示]四个.2.棱柱、棱锥、棱台的结构特征2019-2020年人教B版数学必修二讲义:第1章+1.1+1.1.2棱柱、棱锥和棱台的结构特征及答案-2-/11(1)棱柱的结构特征.定义有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体图示及相关概念底面:两个互相平行的面侧面:底面以外的其余各面侧棱:相邻两侧面的公共边顶点:侧面与底面的公共顶点分类按底面多边形的边数分:三棱柱、四棱柱⋯⋯(2)棱锥的结构特征.定义有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体图示及相关概念底面:多边形面侧面:有公共顶点的各个三角形面侧棱:相邻两侧面的公共边顶点:各侧面的公共顶点分类按底面多边形的边数分:三棱锥、四棱锥⋯⋯(3)棱台的结构特征.定义用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分图示及相关概念上底面:原棱锥的截面下底面:原棱锥的底面侧面:除上下底面以外的面侧棱:相邻两侧面的公共边顶点:侧面与上(下)底面的公共顶点分类按由几棱锥截得分:三棱台、四棱台⋯⋯1.棱锥的侧面和底面可以都是()A.三角形B.四边形C.五边形D.六边形2019-2020年人教B版数学必修二讲义:第1章+1.1+1.1.2棱柱、棱锥和棱台的结构特征及答案-3-/11A[棱锥的侧面都是三角形,所以底面和侧面相同只能是三角形.]2.四棱柱有几条侧棱,几个顶点()A.四条侧棱、四个顶点B.八条侧棱、四个顶点C.四条侧棱、八个顶点D.六条侧棱、八个顶点C[由四棱柱的结构特征知它有四条侧棱,八个顶点.]3.下面四个几何体中,是棱台的是()ABCDC[棱台的侧棱延长后相交于同一点,故C正确.]4.一个棱柱至少有________个面,顶点最少的一个棱台有________条侧棱.53[面最少的棱柱是三棱柱,它有5个面;顶点最少的一个棱台是三棱台,它有3条侧棱.]棱柱、棱锥、棱台的概念【例1】下列关于棱锥、棱台的说法中,正确说法的序号是________.(1)用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;(2)棱台的侧面一定不会是平行四边形;(3)棱锥的侧面只能是三角形;(4)棱台的各侧棱延长后必交于一点;(5)棱锥被平面截成的两部分不可能都是棱锥.(2)(3)(4)[(1)错误,若平面不与棱锥底面平行,用这个平面去截棱锥,棱锥底面和截面之间的部分不是棱台;(2)正确,棱台的侧面一定是梯形,而不是平行四边形;2019-2020年人教B版数学必修二讲义:第1章+1.1+1.1.2棱柱、棱锥和棱台的结构特征及答案-4-/11(3)正确,由棱锥的定义知棱锥的侧面只能是三角形;(4)正确,棱台是由平行于棱锥底面的平面截得的,故棱台的各侧棱延长后必交于一点;(5)错误,如图所示四棱锥被平面PBD截成的两部分都是棱锥.]判断一个几何体是何种几何体,一定要紧扣棱柱、棱锥、棱台的结构特征,注意概念中的特殊字眼,切不可马虎大意,如棱柱的概念中的“相邻”,棱锥的概念中的“公共顶点”,棱台的概念中的“棱锥”“平行”等.1.下列关于棱柱的说法正确的个数是()①四棱柱是平行六面体;②有两个面平行,其余各面都是平行四边形的几何体是棱柱;③有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都...