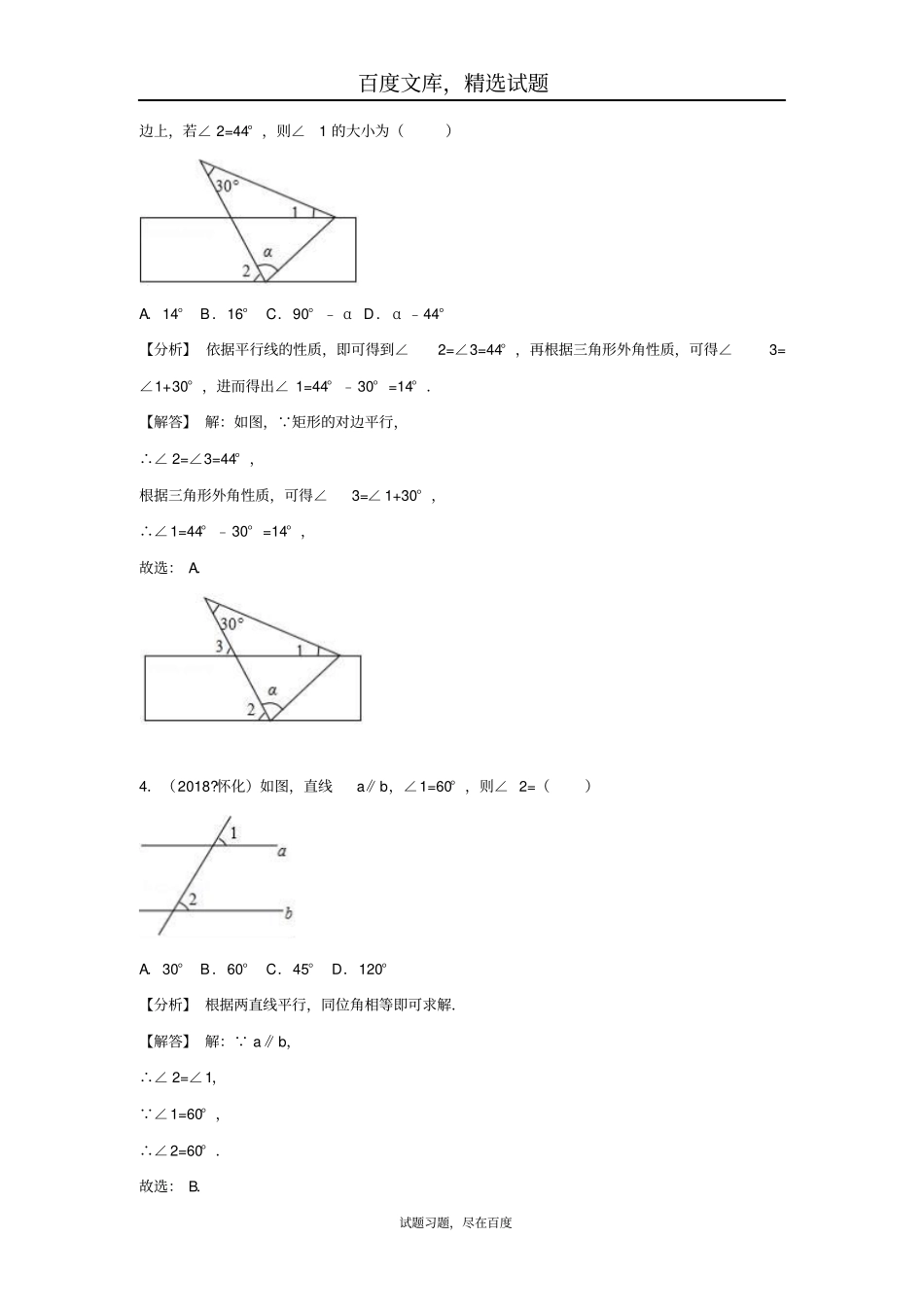
百度文库,精选试题试题习题,尽在百度2018中考数学试题分类汇编:考点18相交线与平行线一.选择题(共30小题)1.(2018?邵阳)如图所示,直线AB,CD相交于点O,已知∠AOD=160°,则∠BOC的大小为()A.20°B.60°C.70°D.160°【分析】根据对顶角相等解答即可.【解答】解: ∠AOD=160°,∴∠BOC=∠AOD=160°,故选:D.2.(2018?滨州)如图,直线AB∥CD,则下列结论正确的是()A.∠1=∠2B.∠3=∠4C.∠1+∠3=180°D.∠3+∠4=180°【分析】依据AB∥CD,可得∠3+∠5=180°,再根据∠5=∠4,即可得出∠3+∠4=180°.【解答】解:如图, AB∥CD,∴∠3+∠5=180°,又 ∠5=∠4,∴∠3+∠4=180°,故选:D.3.(2018?泰安)如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对百度文库,精选试题试题习题,尽在百度边上,若∠2=44°,则∠1的大小为()A.14°B.16°C.90°﹣αD.α﹣44°【分析】依据平行线的性质,即可得到∠2=∠3=44°,再根据三角形外角性质,可得∠3=∠1+30°,进而得出∠1=44°﹣30°=14°.【解答】解:如图, 矩形的对边平行,∴∠2=∠3=44°,根据三角形外角性质,可得∠3=∠1+30°,∴∠1=44°﹣30°=14°,故选:A.4.(2018?怀化)如图,直线a∥b,∠1=60°,则∠2=()A.30°B.60°C.45°D.120°【分析】根据两直线平行,同位角相等即可求解.【解答】解: a∥b,∴∠2=∠1, ∠1=60°,∴∠2=60°.故选:B.百度文库,精选试题试题习题,尽在百度5.(2018?深圳)如图,直线a,b被c,d所截,且a∥b,则下列结论中正确的是()A.∠1=∠2B.∠3=∠4C.∠2+∠4=180°D.∠1+∠4=180°【分析】依据两直线平行,同位角相等,即可得到正确结论.【解答】解: 直线a,b被c,d所截,且a∥b,∴∠3=∠4,故选:B.6.(2018?绵阳)如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是()A.14°B.15°C.16°D.17°【分析】依据∠ABC=60°,∠2=44°,即可得到∠EBC=16°,再根据BE∥CD,即可得出∠1=∠EBC=16°.【解答】解:如图, ∠ABC=60°,∠2=44°,∴∠EBC=16°, BE∥CD,∴∠1=∠EBC=16°,故选:C.百度文库,精选试题试题习题,尽在百度7.(2018?泸州)如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是()A.50°B.70°C.80°D.110°【分析】直接利用角平分线的定义结合平行线的性质得出∠BAD=∠CAD=50°,进而得出答案.【解答】解: ∠BAC的平分线交直线b于点D,∴∠BAD=∠CAD, 直线a∥b,∠1=50°,∴∠BAD=∠CAD=50°,∴∠2=180°﹣50°﹣50°=80°.故选:C.8.(2018?乌鲁木齐)如图把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=()A.20°B.30°C.40°D.50°【分析】根据两直线平行,同位角相等可得∠3=∠1,再根据平角等于180°列式计算即可得解.【解答】解: 直尺对边互相平行,∴∠3=∠1=50°,∴∠2=180°﹣50°﹣90°=40°.故选:C.百度文库,精选试题试题习题,尽在百度9.(2018?孝感)如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为()A.42°B.50°C.60°D.68°【分析】依据三角形内角和定理,即可得到∠ABC=60°,再根据AD∥BC,即可得出∠2=∠ABC=60°.【解答】解: ∠1=42°,∠BAC=78°,∴∠ABC=60°,又 AD∥BC,∴∠2=∠ABC=60°,故选:C.10.(2018?衢州)如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于()A.112°B.110°C.108°D.106°【分析】由折叠可得,∠DGH=∠DGE=74°,再根据AD∥BC,即可得到∠GHC=180°﹣∠DGH=106°.【解答】解: ∠AGE=32°,∴∠DGE=148°,由折叠可得,∠DGH=∠DGE=74°,百度文库,精选试题试题习题,尽在百度 AD∥BC,∴∠GHC=180°﹣∠DGH=106°,故选:D.11.(2018?新疆)如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为()A.85°B.75°C.60°D.30°【分析】先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠...