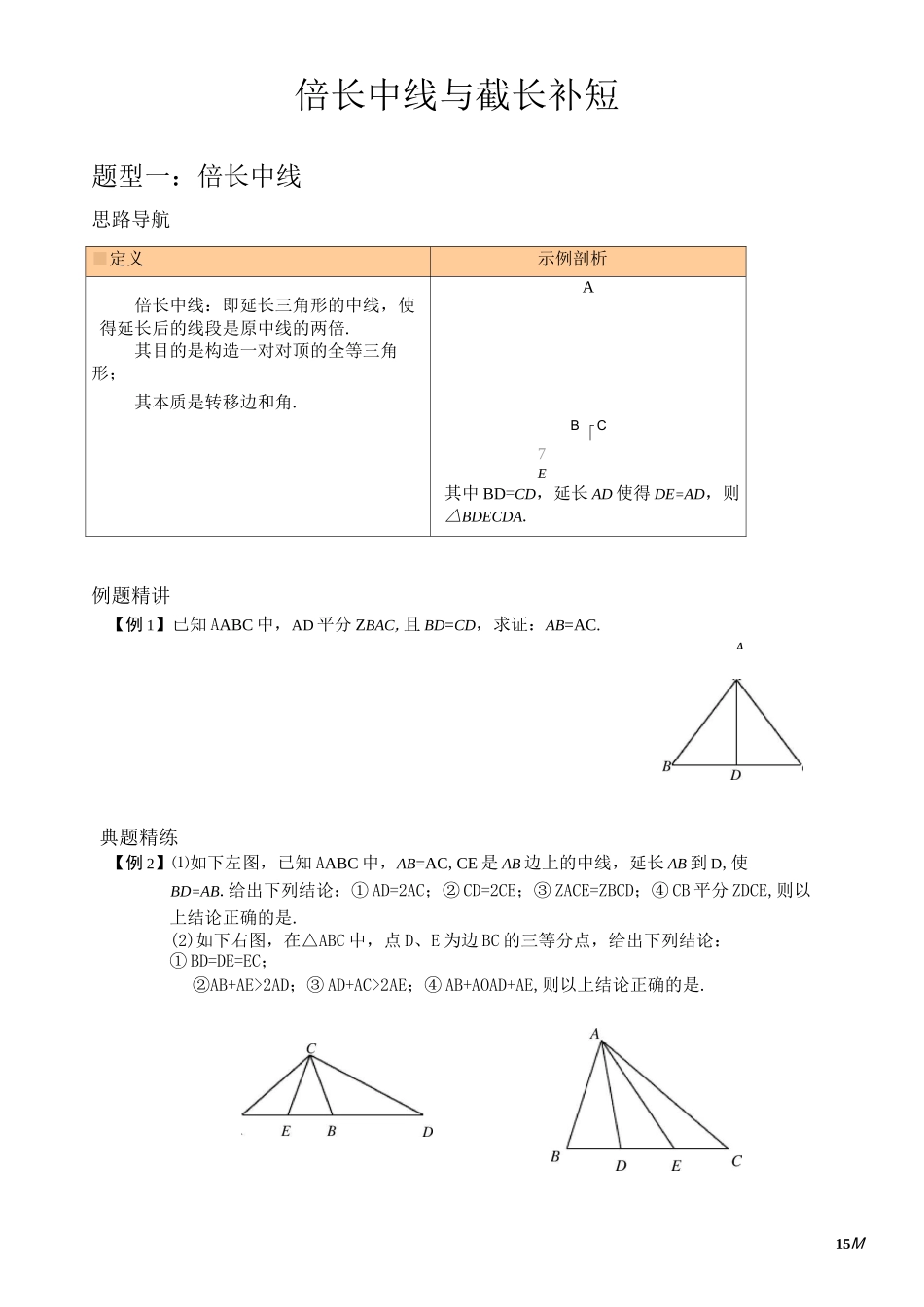
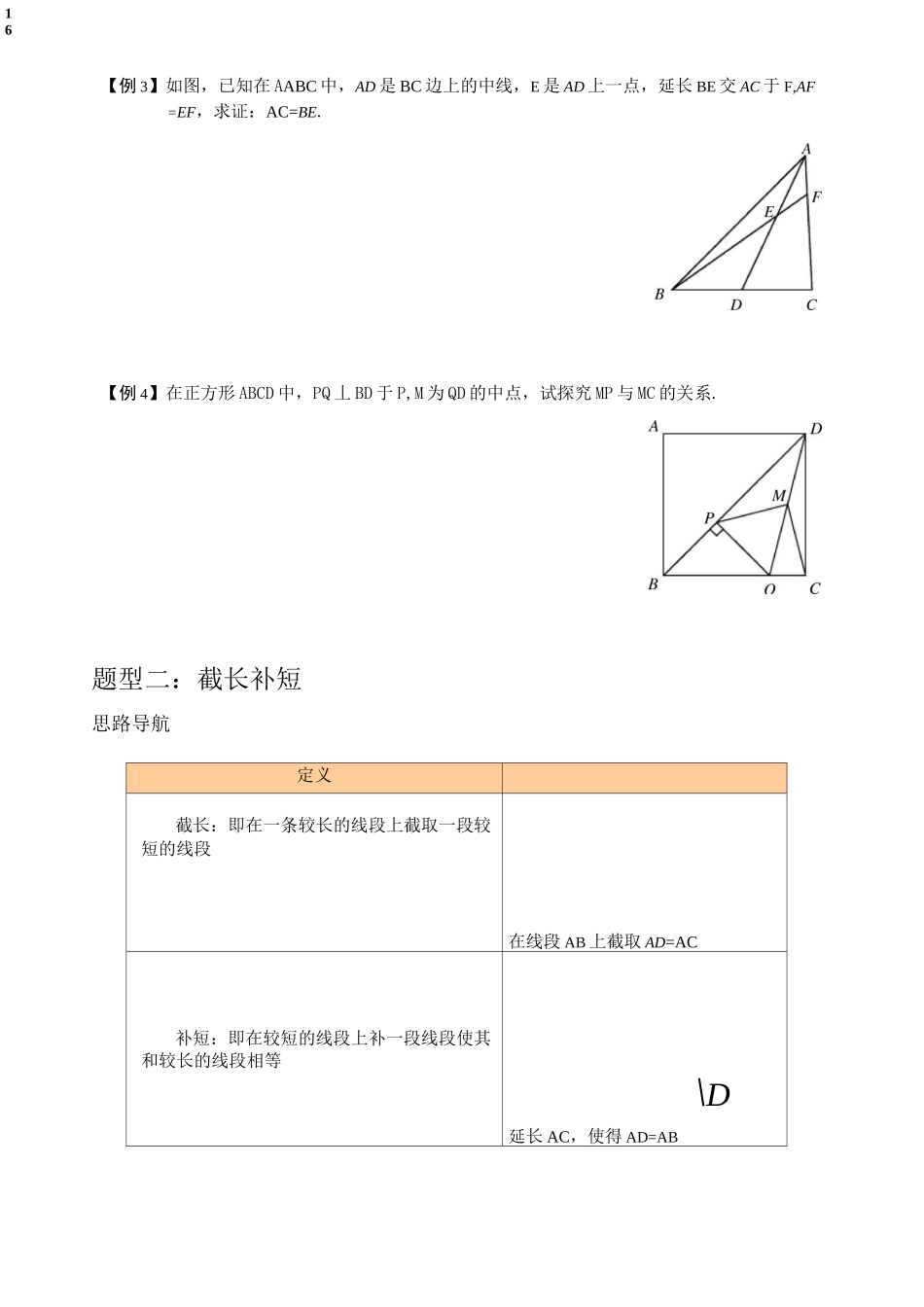
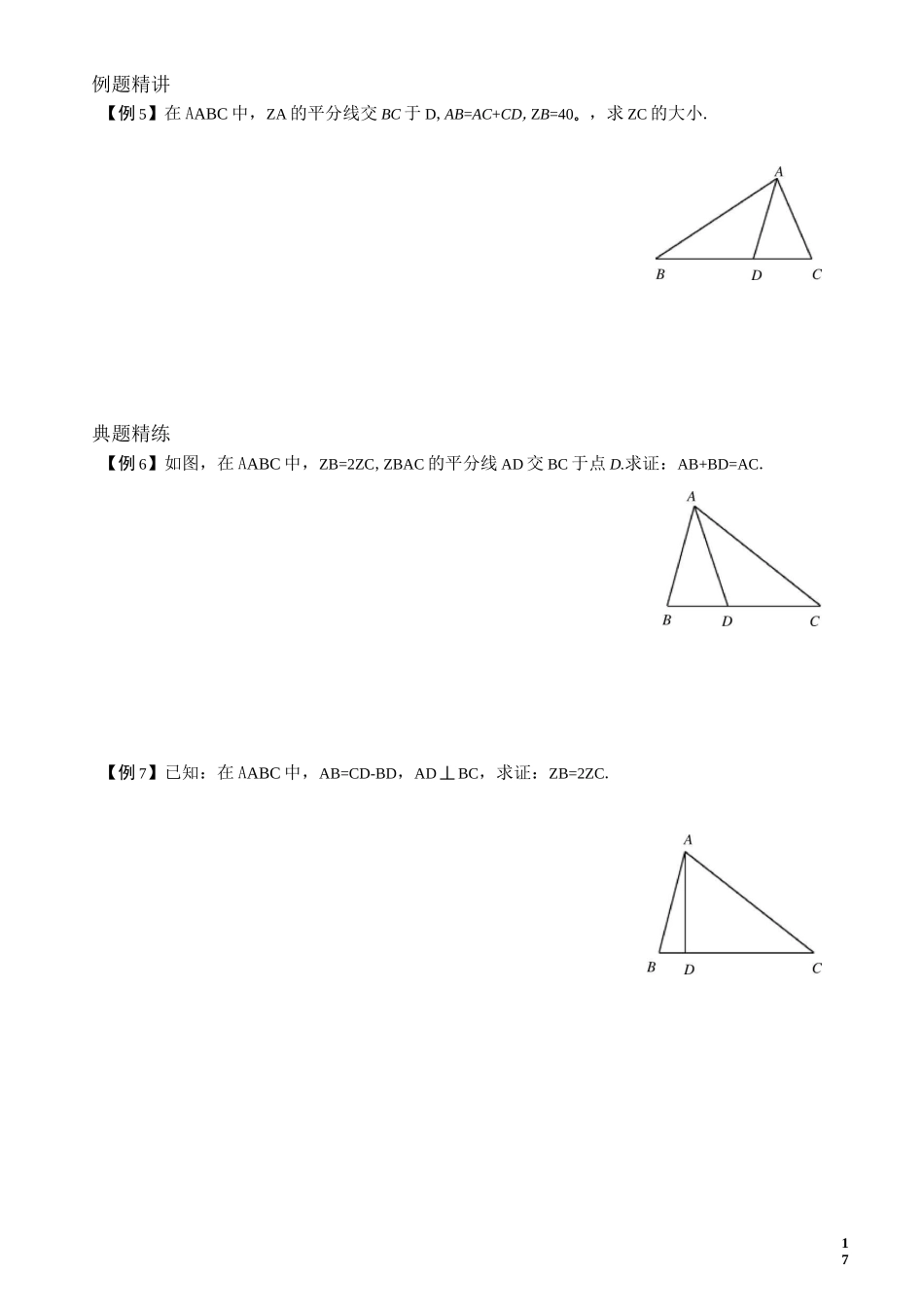
15M倍长中线与截长补短题型一:倍长中线思路导航■定义示例剖析倍长中线:即延长三角形的中线,使得延长后的线段是原中线的两倍.其目的是构造一对对顶的全等三角形;A其本质是转移边和角.B「C7E其中BD=CD,延长AD使得DE=AD,则△BDECDA.例题精讲【例1】已知AABC中,AD平分ZBAC,且BD=CD,求证:AB=AC.典题精练【例2】⑴如下左图,已知AABC中,AB=AC,CE是AB边上的中线,延长AB到D,使BD=AB.给出下列结论:①AD=2AC;②CD=2CE;③ZACE=ZBCD;④CB平分ZDCE,则以上结论正确的是.(2)如下右图,在△ABC中,点D、E为边BC的三等分点,给出下列结论:①BD=DE=EC;②AB+AE>2AD;③AD+AC>2AE;④AB+AOAD+AE,则以上结论正确的是.A16【例3】如图,已知在AABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,AF=EF,求证:AC=BE.【例4】在正方形ABCD中,PQ丄BD于P,M为QD的中点,试探究MP与MC的关系.题型二:截长补短思路导航定义截长:即在一条较长的线段上截取一段较短的线段在线段AB上截取AD=AC补短:即在较短的线段上补一段线段使其和较长的线段相等\D延长AC,使得AD=AB17例题精讲【例5】在AABC中,ZA的平分线交BC于D,AB=AC+CD,ZB=40。,求ZC的大小.典题精练【例6】如图,在AABC中,ZB=2ZC,ZBAC的平分线AD交BC于点D.求证:AB+BD=AC.【例7】已知:在AABC中,AB=CD-BD,AD丄BC,求证:ZB=2ZC.【例18训练训练已知:正方形ABCD中,ZMAN=45°,绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.⑴如图1,当ZMAN绕点A旋转到BM=DN时,有BM+DN=MN.当ZMAN绕点A旋转到BM丰DN时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;⑵当ZMAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间有怎样的等量关系?请写出你的猜想,并证明.已知AD为AABC的中线,ZADB、ZADC的平分线分别交AB于E、交AC于F.求证:BE+CF>EF.如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分ZDAE,求证:AE=EC+CDDCCE19训练3.如图,AABC中,AB=AC,ZA=108。,BD平分ZABC交AC于D点.求证:BC=AC+CD.训练4.五边形ABCDE中,AB=AE,BC+DE=CD,ZABC+ZAED=180°,求证:AD平分ZCDE.复习巩固题型一倍长中线课后演练【演练1】在AABC中,AB=5,AC=9,则BC边上的中线AD的长的取值范围是什么?【演练2】在Rt△ABC中,F是斜边AB的中点,D、E分别在边CA、CB上,满足ZDFE=90。.若AD=3,BE=4,则线段DE的长度为.20题型二截长补短课后演练【演练3】如图,点M为正三角形ABD的边AB所在直线上的任意一点(点B除外),作ZDMN=60。,射线MN与ZDBA外角的平分线交于点N,DM与MN有怎样的数量关系?(提示:过点M作MG〃BD交AD于点G)【演练4】如图所示,已知AABC中,AC=BC,ZC=90。,AD平分ZBAC,求证:AC+CD=AB.【演练5】已知:如图,ABCD是正方形,ZFAD=ZFAE.求证:BE+DF=AE.