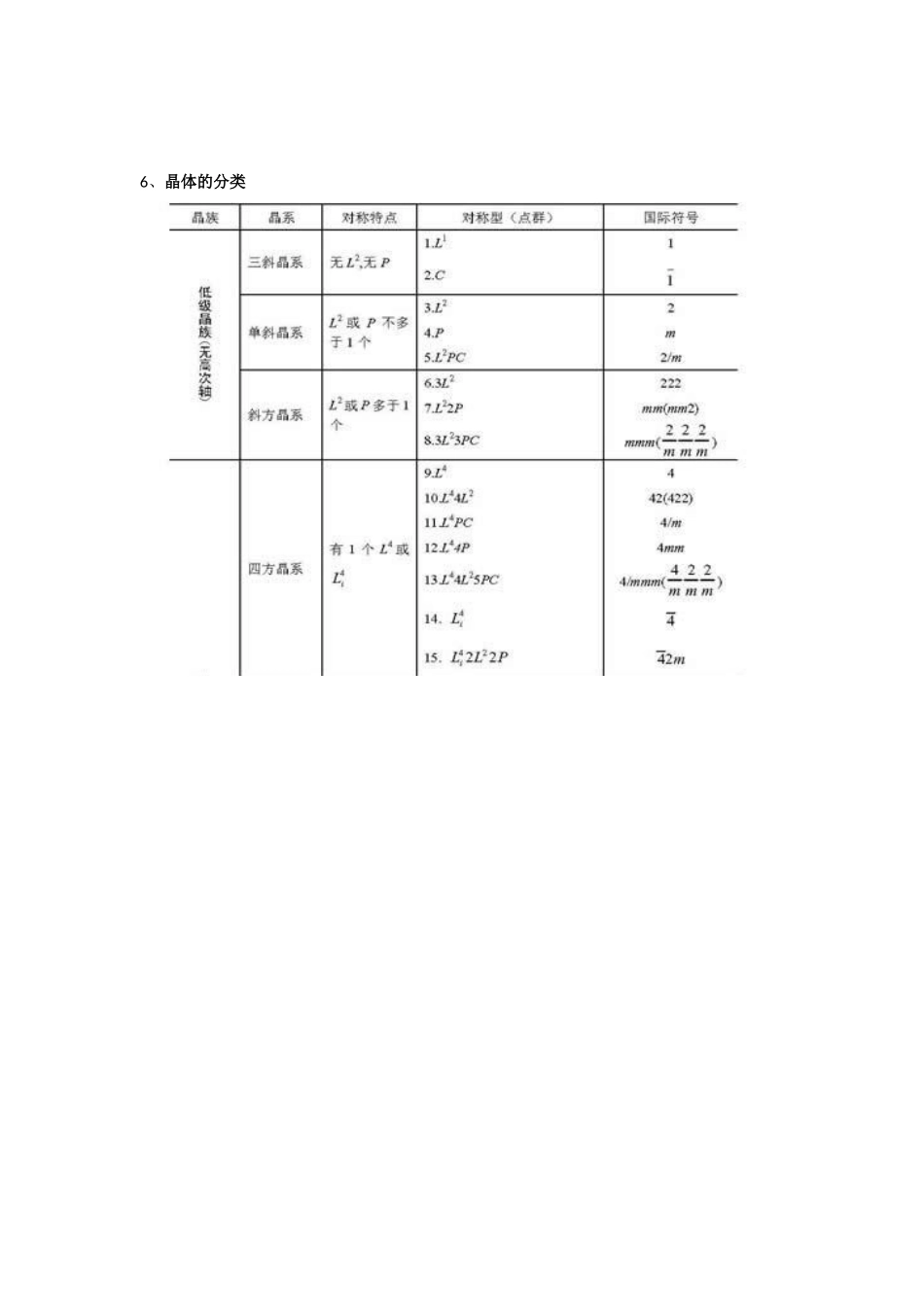
1、结晶学:以晶体为研究对象,以晶体的对称规律为主要研究内容的一门基础基础性的自然科学。2、矿物学:以矿物晶体为研究对象,主要研究各具体矿物晶体的成分、物理性质、成因特点等。3、晶体:内部结构具有周期重复性,即具有格子构造的固体。晶体结构=点阵(或空间格子)+结构基元4、格子构造:晶体结构的周期重复规律,这种规律是可以用格子状的图形-空间格子表示的。5、空间格子:表示晶体结构周期重复规律的简单几何图形。6、相当点:满足以下两个条件的点:性质相同,周围环境相同。7、空间格子的四要素①结点:空间格子中的点,代表具体晶体结构中的相当点。结点间距:同一行列中相邻结点间的距离。②行列:结点在直线上的排列。③面网:结点在平面上的分布。面网密度:面网上单位面积内结点的密度。面网间距:任意两相邻面网间的垂直距离。(面网密度与面网间距成正比)④平行六面体:结点在三维空间形成的最小重复单位。平行六面体对应的实际晶体中相应的范围叫晶胞。8、晶体的基本性质①自限性:晶体能够自发地生长成规则的几何多面体形态。②均一性:同一晶体的不同部分物理化学性质完全相同。晶体是绝对均一性,非晶体是统计的、平均近似均一性。③异向性:同一晶体不同方向具有不同的物理性质。例如:蓝晶石的不同方向上硬度不同。④对称性:同一晶体中,晶体形态相同的几个部分(或物理性质相同的几个部分)有规律地重复出现。⑤最小内能性:晶体与同种物质的非晶体相比,内能最小。晶体具有固定的熔点。⑥稳定性:晶体比具有相同化学成分的非晶体稳定。1、实际晶体形态(歪晶):偏离理想的晶体形态。2、面角守恒定律:同种矿物的晶体,其对应晶面间的角度守恒。(意义:结晶学发展的奠基石)3、晶体测量:就是测量晶面之间的夹角。方法:①接触测角(接触测角仪)②反射测角(单圈、双圈反射测角仪)4、晶体的投影:将晶面的空间分布转化为平面图。①极射赤平投影:晶面的球面投影,晶体的球面坐标,晶体的极射赤平投影,吴氏网②心射极平投影1、对称:物体相同部分有规律的重复。2、晶体对称的特点。①由于晶体内部都具有格子构造,通过平移,可使相同质点重复,因此,所有的晶体结构都是对称的(这种对称叫平移对称)。②晶体的对称受格子构造规律的限制,因此,晶体的对称是有限的,它遵循“晶体对称定律”。③晶体的对称不仅体现在外形上,同时也体现在物理性质上。Ps:格子构造使得所有晶体都是对称的,格子构造也使得并不是所有对称都能在晶体中出现的。3、晶体的宏观对称要素和对称操作对称操作:使对称图形中相同部分重复的操作。对称要素:在进行对称操作时所应用的辅助几何要素(点、线、面)。①对称面—P操作为反映。可以有多个对称面存在,如3P、6P等。②对称轴—Ln操作为旋转。其中n代表轴次,意指旋转360度相同部分重复的次数。旋转一次的角度为基转角α,关系为:n=360/α。N>2为高次轴,n<=2为低次轴。晶体的对称定律:由于晶体是具有格子构造的固体物质,这种质点格子状的分布特点决定了晶体的对称轴只有n=1,2,3,4,6这五种,不可能出现n=5,n>6的情况。③对称中心—C操作为反伸。只可能在晶体中心,只可能一个。④旋转反伸轴–Lin操作为旋转+反伸的复合操作。关系:Li1=C,Li2=P,Li3=L3+C,Li6=L3+P4、对称要素的组合①定理1:Ln×L2→LnnL2(L2与L2的夹角是Ln基转角的一半)逆定理:L2与L2相交,在其交点且垂直两L2会产生Ln,其基转角是两L2夹角的两倍。并导出n个在垂直Ln平面内的L2。例:L4×L2→L44L2,L3×L2→L33L2②定理2:Ln×P⊥→LnP⊥C(n为偶数)逆定理:Ln×C→LnP⊥C(n为偶数)P×C→L2P⊥C这一定理说明了L2、P、C三者中任两个可以产生第三者。③定理3:Ln×P//→LnnP//(P与P夹角为Ln基转角的一半);逆定理:两个P相交,其交线必为一Ln,其基转角为P夹角的两倍,并导出n个包含Ln的P。④定理4:Lin×P//=Lin×L2⊥→Linn/2L2⊥n/2P//(n为偶数)→LinnL2⊥nP//(n为奇数)5、32种对称型(点群及其推导)p36对称型(或点群):晶体形态中,全部对称要素的组合。一般来说强调对称要素时称对称型,强调对称操作时称点群。6、晶体的分类1、选...