量子习题解答VIP免费

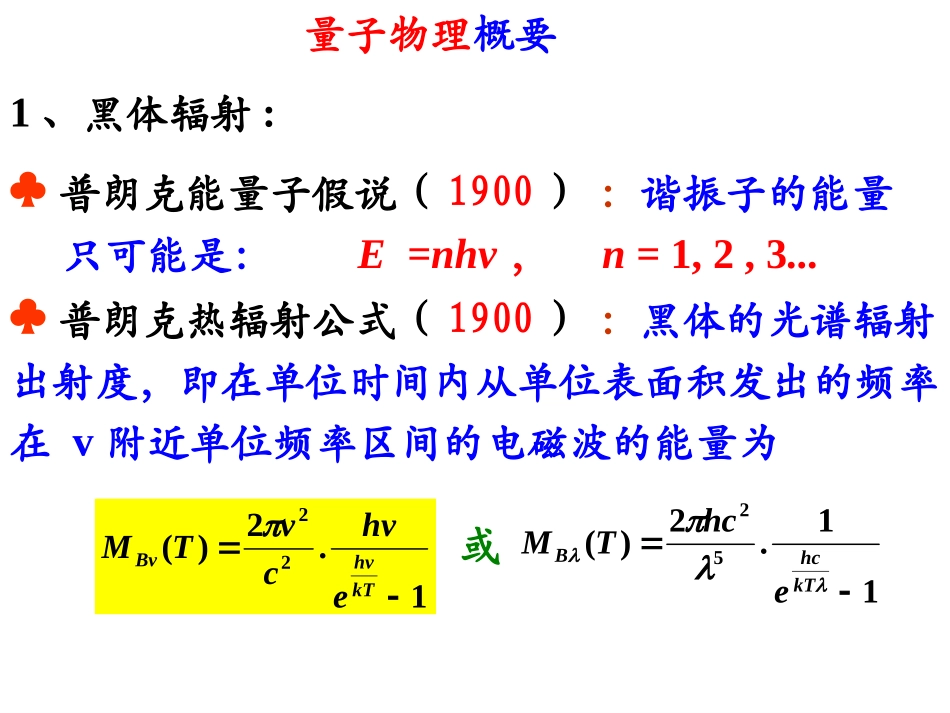
波粒二象性概要2、光电效应：Ahνmvmax221红限频率v0=A/h1、光的粒子性:pcmchE23、康普顿散射：X光经散射有两种成分波长不变波长变长——康普顿散射)cos1(00cmh(康普顿散射公式)2chmhchp4、德布罗意假设：p/hh/E5、物质波波函数Ψ=Ψ(x,y,z,t):(1)单值、有限、连续(2)|Ψ|2为概率密度.1)3(2归一化条件dxdydz6、不确定关系：),(2hpxx或或2h量子物理概要1、黑体辐射:普朗克能量子假说（1900）：谐振子的能量只可能是：E=nhv，n=1,2,3...普朗克热辐射公式（1900）：黑体的光谱辐射出射度，即在单位时间内从单位表面积发出的频率在v附近单位频率区间的电磁波的能量为11.2)(52kThcBehcTM1.2)(22kThvBvehvcvTM或斯特藩-玻耳兹曼定律：黑体对所有频率总的辐射出射为s=5.67×10W·m·K-8b=2.898×10m·K-3TCvmKHzCv/10880.510维恩位移定律：普朗克公式对v（）求导，可得维恩位移定律，即光谱辐射出射度最大的光频率或峰值波长为维恩位移定律：普朗克公式对v（）求导，可得维恩位移定律，即光谱辐射出射度最大的光频率或峰值波长为维恩位移定律：普朗克公式对v（）求导，可得维恩位移定律，即光谱辐射出射度最大的光频率或峰值波长为光电效应（1921）：Ahνmvmax221红限频率v0=A/h爱因斯坦光量子假说（1905）:pcmchE2康普顿散射（1923）：)cos(cmh1002chmhchp2、光的粒子性:4、不确定关系(1927)：),(2hpxx或或2h5、氢原子光谱(1913)2211()()()RTmTnmnmnhEE2nnmvrn谱线的波数频率条件：角动量量子化条件：2/tE位置动量不确定关系：能量时间不确定关系：6、薛定谔方程(1926)（一维）),(,2222txtiUxm定态薛定谔方程（一维）：/222)(,2iEtexEUxm7、薛定谔方程举例（一维）一维无限深势阱中的粒子能量量子化1222222EnnmaE德布罗意波长量子化knan2/2类似于经典的两端固定的弦驻波...3,2,1sin2naxnax00≤x≤ax<0,x>a本本本本势垒穿透：微观粒子可以进入其势能（有限的）大于其总能量的区域，这是由不确定关系决定的。在势垒有限的情况下，粒子可以穿过势垒到达另一侧，这种现象又称隧道效应。谐振子能量量子化...3,2,1,0,)21(nhvnE零点能hvE2108、氢原子：氢原子能级：4222201113.6(eV)2(4)nmeEnn轨道角动量(1)Lll轨道角动量沿磁场方向分量：zLm主量子数n=1,2,3…轨道量子数l=0,1,2,3…,n-1轨道磁量子数ml=-l,-(l-1),…,0,1,..,l9、电子自旋(1926)电子自旋角动量21,43)1(sssS电子自旋在空间某一方向的投影szmSms只有1/2（向上）和-1/2（向下）两个值，为自旋磁量子数。轨道角动量和电子自旋角动量的合角动量2121,)1(ljljjjSLJ和玻尔磁子TJmeeB/1027.9224电子自旋磁矩在磁场中的能量BEBs10、多电子原子的电子组态电子的状态用4个量子数n,l,ml,ms确定。n相同的状态组成一壳层，可容纳2n2个电子；l相同的状态组成一次壳层，可容纳2（2l+1)个电子。基态原子电子组态遵循两个规律：（1）能量最低原理，即电子总处于可能最低的能级。一般n越大，l越大，能量就越高。（2）泡利不相容原理(1921)，不可能有两个或两个以上的电子处在同一量子状态。即不能有两个电子具有相同的n,l,ml,ms。例1黑体辐射例题实验测得太阳单色辐出度峰值对应的波长若将太阳当作黑体，估算：490nm（1）太阳表面的温度T。（2）太阳辐出度。解：（1）由维恩位移定律得：490×10_95.91×103(K)2.898×10_3（2）斯特藩-玻耳兹曼定律得：5.67×10×(5.91×10)_83476.92×10(W·m)_2例2（19届12题）对太阳光谱的强度分析，确认太阳辐射本领的峰值在465nm处。将太阳处理为黑体，可知太阳表面温度为_________K，单位面积上辐射功率为_________W/m2,(斯忒藩-玻耳兹曼常数维恩常数b=2.898×10-3mK)。)Km(105.670428...