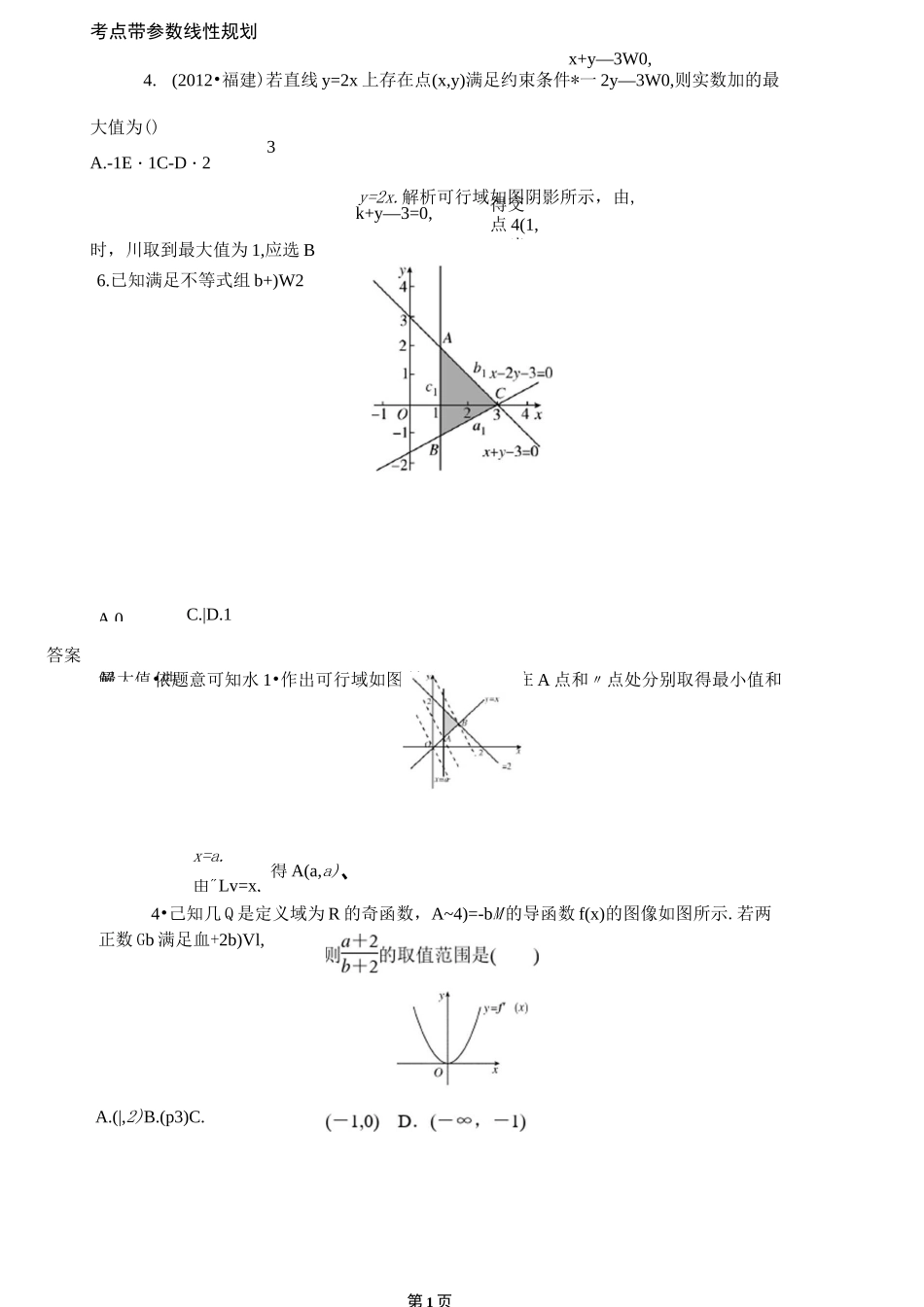
第1页得交点4(1,2),当6.已知满足不等式组b+)W2t且z=2x+y的A.0解最大值•曲依题意可知水1•作出可行域如图所示,Z=2x+y在A点和〃点处分别取得最小值和x+y=2,‘1x=a.得A(a,a)、由"Lv=x,考点带参数线性规划x+y—3W0,4.(2012•福建)若直线y=2x上存在点(x,y)满足约束条件*一2y—3W0,则实数加的最大值为()3A.-1E・1C-D・2y=2x.解析可行域如图阴影所示,由,k+y—3=0,时,川取到最大值为1,应选BC.|D.1答案4•己知几Q是定义域为R的奇函数,A~4)=-bM的导函数f(x)的图像如图所示.若两正数Gb满足血+2b)Vl,A.(|,2)B.(p3)C.第1页的内:・kpBOtQO)的最人值为12,23则缶的最小值为(258B3c.yD・4答案A作可目标第2页答案B解析••了⑴是定义域为R的奇函数,A-4)=-b•••/(一4)=一/(4),・説4)=1.:.J(a+2b)一1.・.$“必=2,.•.|(l+n)Xl=2,解得a=3.!2A—y+l>0,x+加<0,表示的平面区域内存在点P(.m,yo),y—m>Q满足-Vo—2yo=2,求得加的取值范闱是()A.(-8,I)B.(-8,dc(—8,D.(-8,_D答案C解析当加20时,若平面区域存在,则平面区域内的点在第二象限,平面区域内不可能存在点P(Xo,)9)满足x0—2)'0=2,因此加<0.如图所示的阴影部分为不等式组表示的平面区域.要使可行域内包含y=p-1上的点,只需可行域边界点(-/«,m)在直线y=p-l的下方即_12可,即in<—尹2—1,解得m<—y5.(2013-课标全国II)已知a>0,x,y满足约束条件