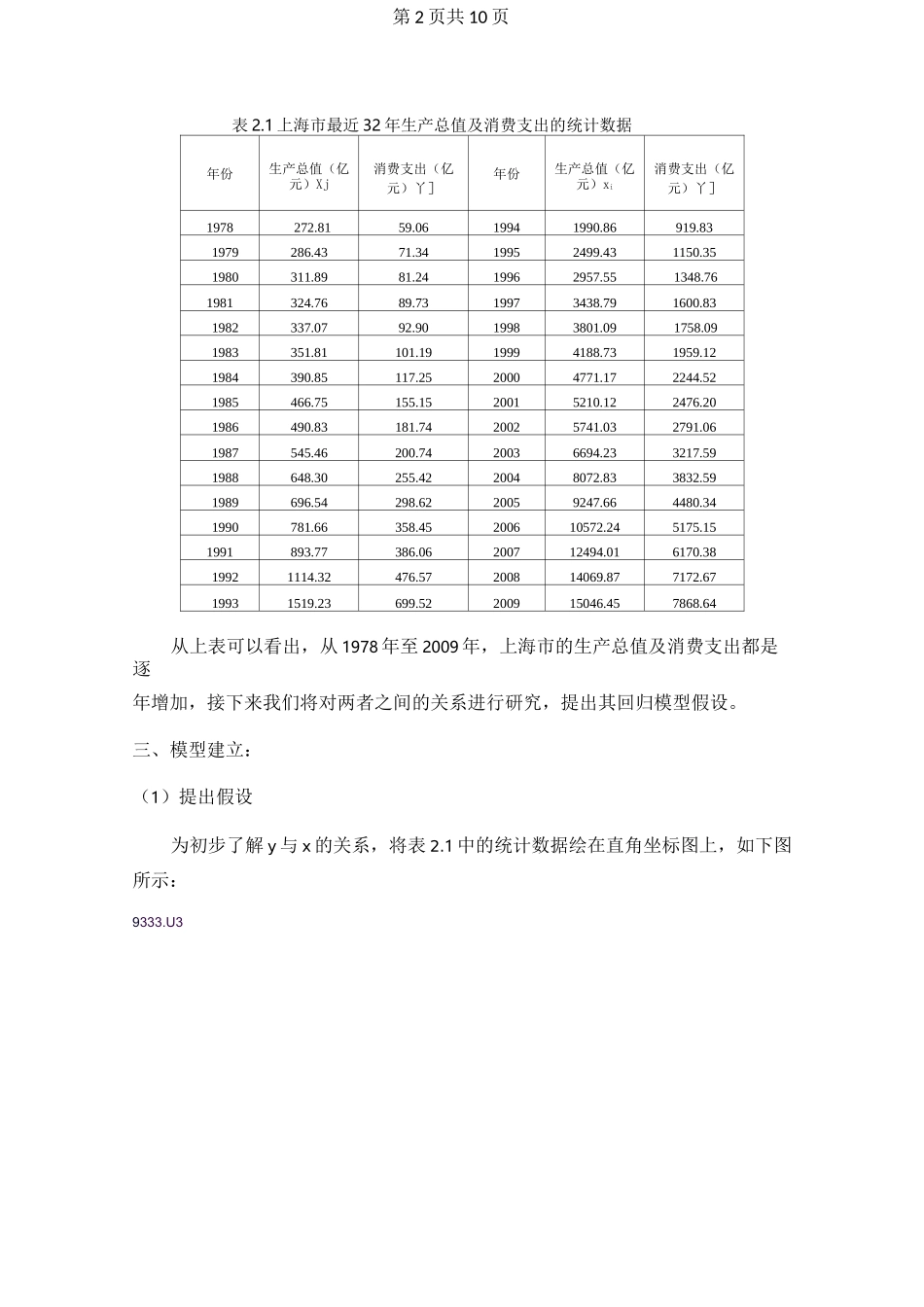
第1页共10页上海市生产总值与消费支出的回归计算分析摘要:本文从《上海统计年鉴2010》中获取原始数据,对上海市生产总值与消费支出进行回归计算分析,首先在直角坐标上绘制散点图,提出一元线性回归的模型假设,然后进行模型求解,最后通过计算机利用Exce丨软件,绘制“残差图”、“线性拟合图”及“正态概率图”,用以判定假设模型的实用性,最终得出的结论是虽然两者拟合的情况很好,但据残差分析,回归分析模型假定方差齐性有出入,故原假设模型不成立,原因是计量经济学有很多不确定性影响因素,预测的结果也是概率意义上的。在以后的数据分析中,我们有必要对残差分析加以重视。一、引言上海市的生产总值即通常所说的GDP,很多人会关心它的增长速度,但也许未必知道它的用途。统计专家告诉我们,GDP的生产、分配和使用各个环节所表现出来的经济现象互为因果,相互作用,只有当各种经济关系的比例比较协调时,才能达到经济运作机制的良性循环和实现可持续发展。那么上海的GDP是怎么用的,它与消费支出又有什么关系呢?下面我们将对上海市1978~2009年的统计数据进行分析,运用数理统计的知识,来探究其生产总值与消费支出的回归模型。二、数据描述依据《上海统计年鉴2010》表3.13上海市生产总值(支出法)(1978~2009)和表3.14最终消费支出及构成(1978~2009),获取上海市最近32年生产总值及消费支出的统计数据,如下表所示:第2页共10页表2.1上海市最近32年生产总值及消费支出的统计数据年份生产总值(亿消费支出(亿年份生产总值(亿消费支出(亿元)Xj元)丫]元)xi元)丫]1978272.8159.0619941990.86919.831979286.4371.3419952499.431150.351980311.8981.2419962957.551348.761981324.7689.7319973438.791600.831982337.0792.9019983801.091758.091983351.81101.1919994188.731959.121984390.85117.2520004771.172244.521985466.75155.1520015210.122476.201986490.83181.7420025741.032791.061987545.46200.7420036694.233217.591988648.30255.4220048072.833832.591989696.54298.6220059247.664480.341990781.66358.45200610572.245175.151991893.77386.06200712494.016170.3819921114.32476.57200814069.877172.6719931519.23699.52200915046.457868.64从上表可以看出,从1978年至2009年,上海市的生产总值及消费支出都是逐年增加,接下来我们将对两者之间的关系进行研究,提出其回归模型假设。三、模型建立:(1)提出假设为初步了解y与x的关系,将表2.1中的统计数据绘在直角坐标图上,如下图所示:9333.U3第3页共10页图3.1上海市生产总值x与消费支出y的散点图由图3.1可见,上海市生产总值x与消费支出y的关系式可以用线性方程来拟合,初步假定其关系为:y=+M(2)模型构建由上述假设提出一元线性回归模型:|Y=p0+P1x+EY对x的一元线性回归方程为:y=^=^-^±x其中错误!未找到引用源。、错误!未找到引用源。称为回归系数,常数错误!未找到引用源。、错误!未找到引用源。、错误!未找到引用源。均未知。(3)模型求解设错误!未找到引用源。为取得的一组试验数据,假定满足如下一元线性回归模型:71=Pto+阻绚一斫,i=1,2,--,11,SL-N(O,S2),i=1T2;■■-J5車(%号)=0’i=j,i」j=lZ…4需要在此基础上确定回归系数错误!未找到引用源。、错误!未找到引用源。的估计值错误!未找到引用源。,并使残差第4页共10页-二二-兀■=--'■-尽可能小,其中或=爲+宵舌佢=训…小)称为错误!未找到引用源。的预测值,由此得到的r=£+M称为样本回归直线或经验回归直线。米用最小二乘法,令n时=》〔肌一BQ—旳终)21=1求解下面的优化问题n皿也賂也》Cyi-Po-P^)21=1最终求解出错误!未找到引用源。、错误!未找到引用源。,简记为LTD=y-^利用Exce1对表2.1中的统计数据进行计算,详见附录A:上海市生产总值与消费支出的回归计算(1978〜2009),其线性回归方程的计算过程如下:错误!未找到引用源。,错误!未找到引用源。;ky=^xlyl-32x-y=516B21777.71-32x3757.14x1805.97i=i=299692749.70S2咕二工£j32S2=1040748299.87-32x3757.142i=l=5S9033068.51错误!未找到引用源。二152705970.34第5页共10页错误!未找...