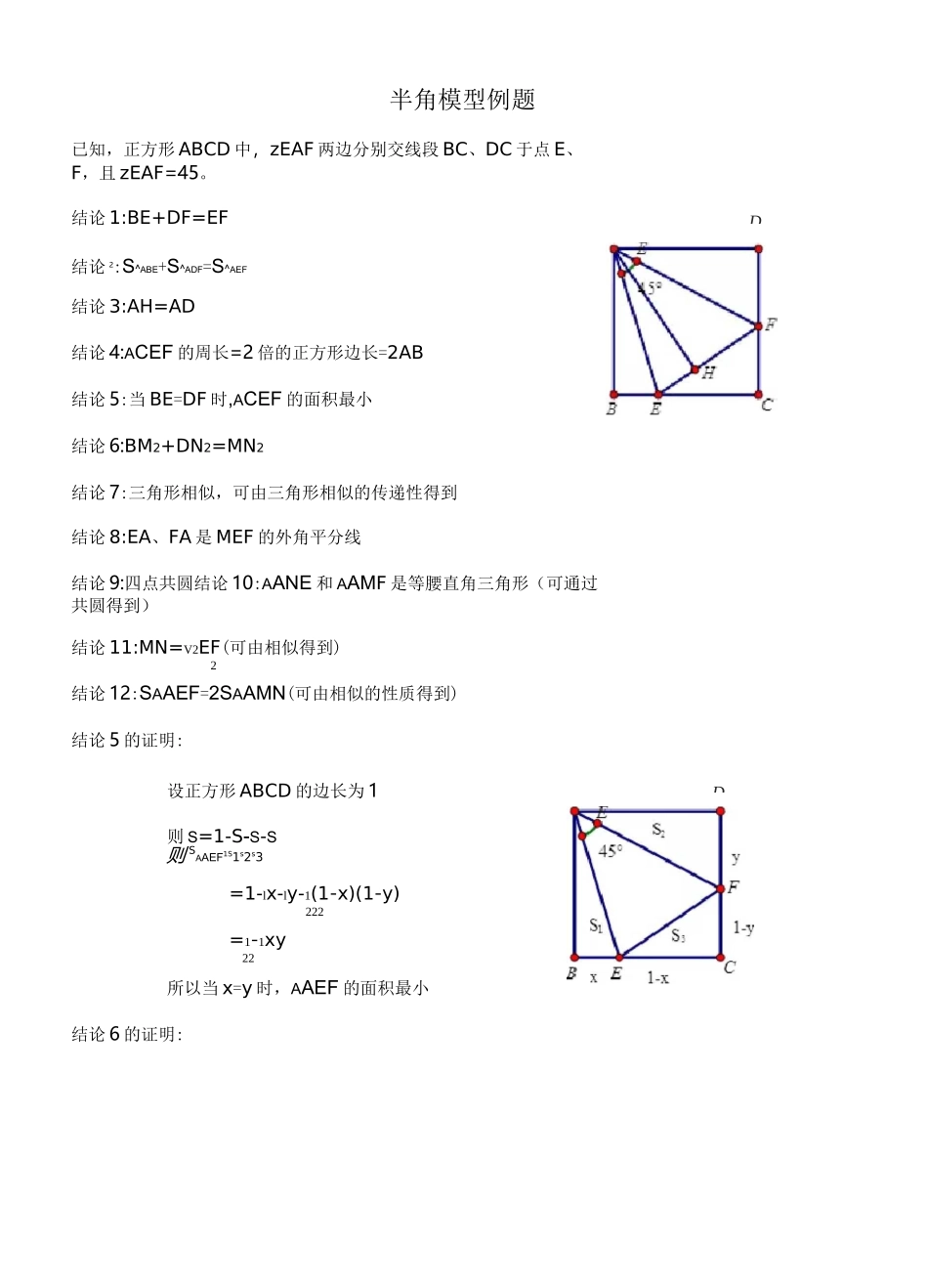
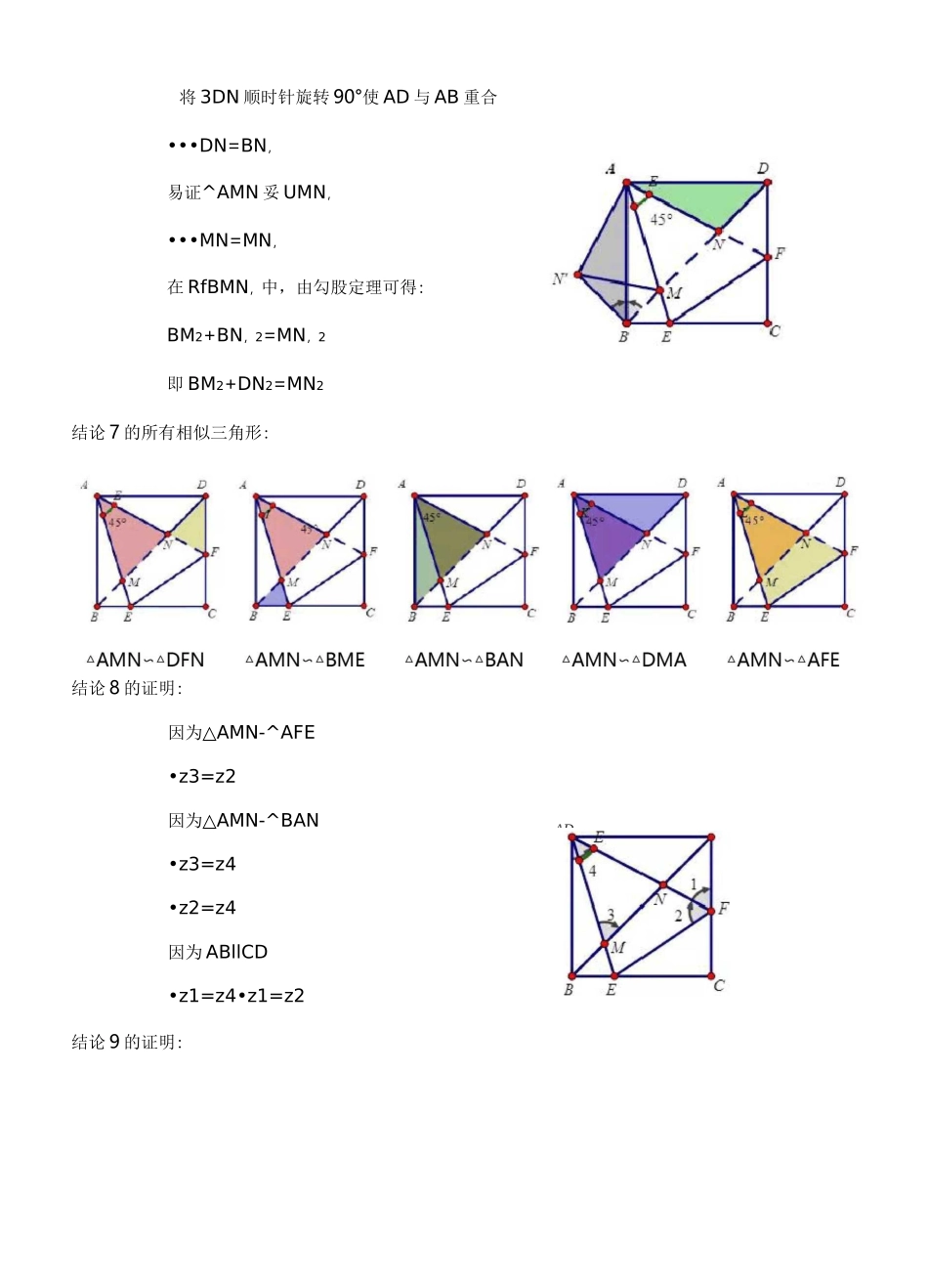
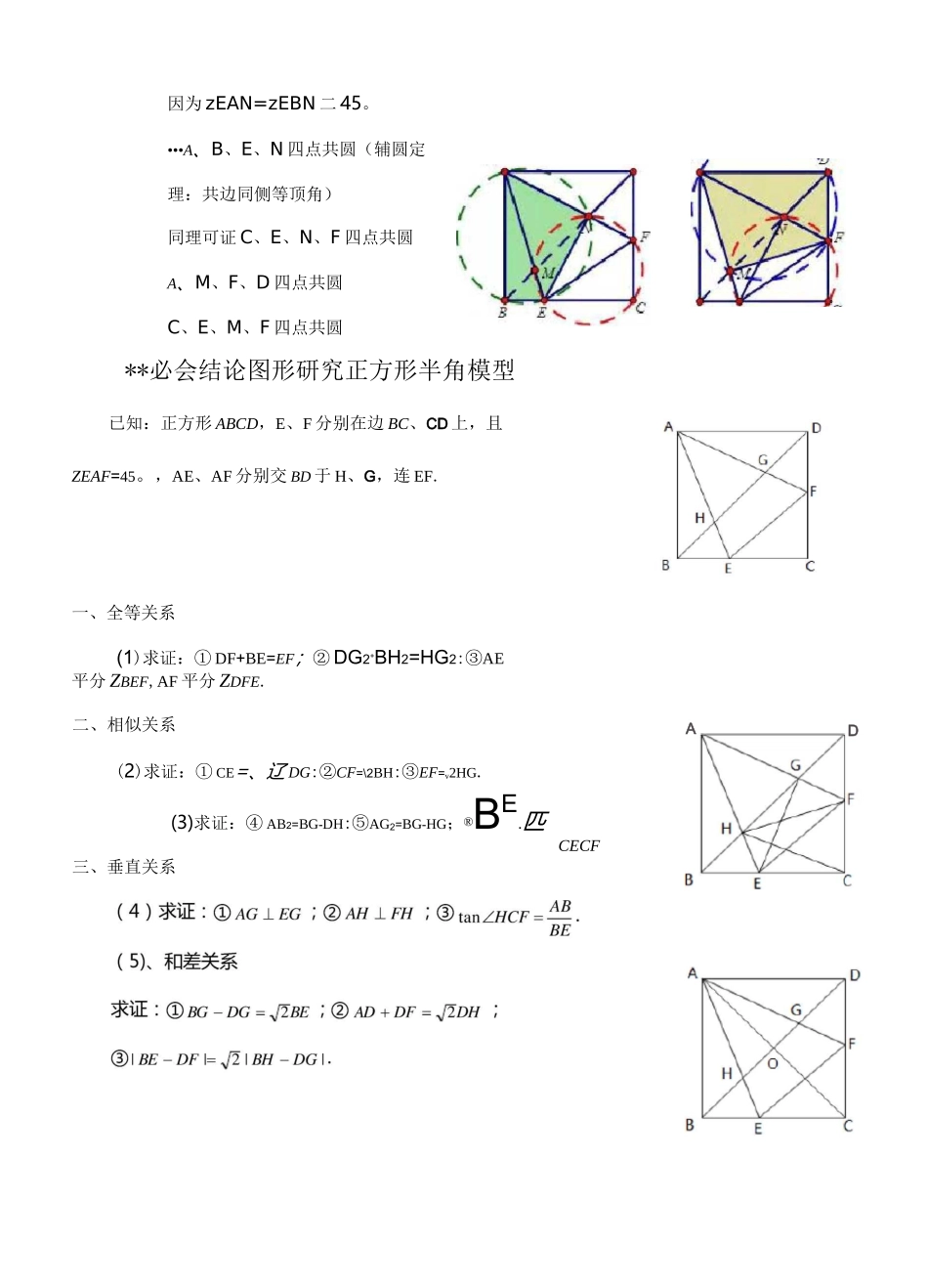
半角模型例题已知,正方形ABCD中,zEAF两边分别交线段BC、DC于点E、F,且zEAF=45。结论1:BE+DF=EF结论2:S^ABE+S^ADF=S^AEF结论3:AH=AD结论4:ACEF的周长=2倍的正方形边长=2AB结论5:当BE=DF时,ACEF的面积最小结论6:BM2+DN2=MN2结论7:三角形相似,可由三角形相似的传递性得到结论8:EA、FA是MEF的外角平分线结论9:四点共圆结论10:AANE和AAMF是等腰直角三角形(可通过共圆得到)结论11:MN=V2EF(可由相似得到)2结论12:SAAEF=2SAAMN(可由相似的性质得到)结论5的证明:设正方形ABCD的边长为1则S=1-S-S-S则SAAEF1S1s2s3=1-lx-ly-1(1-x)(1-y)222=1-1xy22所以当x=y时,AAEF的面积最小结论6的证明:DD将3DN顺时针旋转90°使AD与AB重合•••DN=BN,易证^AMN妥UMN,•••MN=MN,在RfBMN,中,由勾股定理可得:BM2+BN,2=MN,2即BM2+DN2=MN2结论7的所有相似三角形:结论8的证明:因为△AMN-^AFE•z3=z2因为△AMN-^BAN•z3=z4•z2=z4因为ABllCD•z1=z4•z1=z2结论9的证明:AD因为zEAN=zEBN二45。•••A、B、E、N四点共圆(辅圆定理:共边同侧等顶角)同理可证C、E、N、F四点共圆A、M、F、D四点共圆C、E、M、F四点共圆**必会结论图形研究正方形半角模型已知:正方形ABCD,E、F分别在边BC、CD上,且ZEAF=45。,AE、AF分别交BD于H、G,连EF.一、全等关系(1)求证:①DF+BE=EF;②DG2+BH2=HG2:③AE平分ZBEF,AF平分ZDFE.二、相似关系(2)求证:①CE=、辽DG:②CF=\2BH:③EF=v2HG.(3)求证:④AB2=BG-DH:⑤AG2=BG-HG;®BE.匹CECFDA三、垂直关系例1、在正方形ABCD中,已知ZMAN=45°,若M、N分别在边CB、DC的延长线上移动,①•试探究线段MN、BM、DN之间的数量关系.②.求证:AB=AH.例2、在四边形ABCD中,zB+zD=180°,AB=AD,若E、F分别在边BC、CD上,且满足EF=BE+DF.求证:zEAF二izBAD2例3在^ABC中AB二ACzBAC=2zDAE=120°若BD=5,CE=8,求DE的长。例4、请阅读下列材料:已知如图1在RtAABC中,ZBAC=90o,AB=AC点D、E分别为线段BC上两动点,若ZDAE=45。探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把AAEC绕点A顺时针旋转90o,得到AABE',连结ED,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,并对你的猜想给予证明;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图2,其它条件不变,⑴中探究的结论是否发生改变?请说明你的猜想并给予证明.例5、探究:(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且zEAF二45。,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果:;(2)如图2,若把⑴问中的条件变为“在四边形ABCD中,AB=AD,zB+zD=180°,E、F分别是边BC、CD上的点,且zEAF=1zBAD”,则(1)问中的结论是否仍然成立?若成立,请2给出证明,若不成立,请说明理由;(3)在(2)问中,若将MEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明..A图1练习巩固2:如图,在五边形ABCDE中,AB=BC=CD=DE=EA,zCAD二1ZBAE,求zBAE的度数2练习巩固3:已知:正方形ABCD中,ZMAN=45,绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.(1)如图1,当ZMAN绕点A旋转到BM=DN时,有BM+DN=MN•当ZMAN绕点A旋转到BM丰DN时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)当ZMAN绕点A旋转至IJ如图3的位置时,线段BM,DN和MN之间有怎样的等量关系?请写出你的猜想,并证明.练习巩固4⑴如图,在四边形ABCD中,AB=AD,zB=zD=90°,E、F分别是边BC、CD上的点,且zEAF二1zBAD.2求证:EF=BE+FD;⑵如图在四边形ABCD中,AB=AD,zB+zD=180°,E、F分别是边BC、CD上的点,且zEAF=lzBAD,1)中的结论是否仍然成立?2不用证明.⑶如图,在四边形ABCD中,AB=AD,zB+zADC=180°,E、F分别是边BC、CD延长线上的点,且zEAF=1zBAD,(1)中的结论是2否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.(4)如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交...