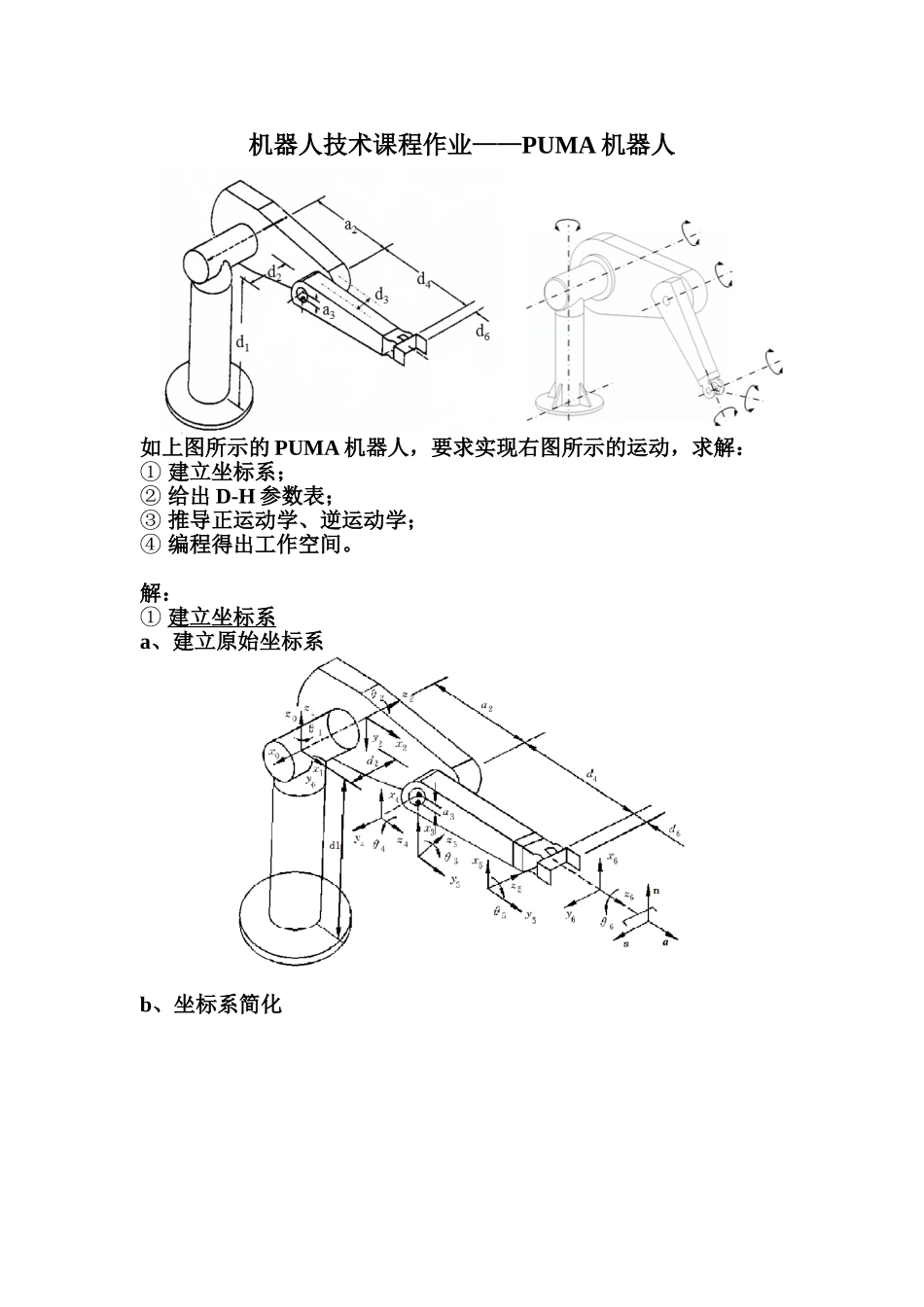
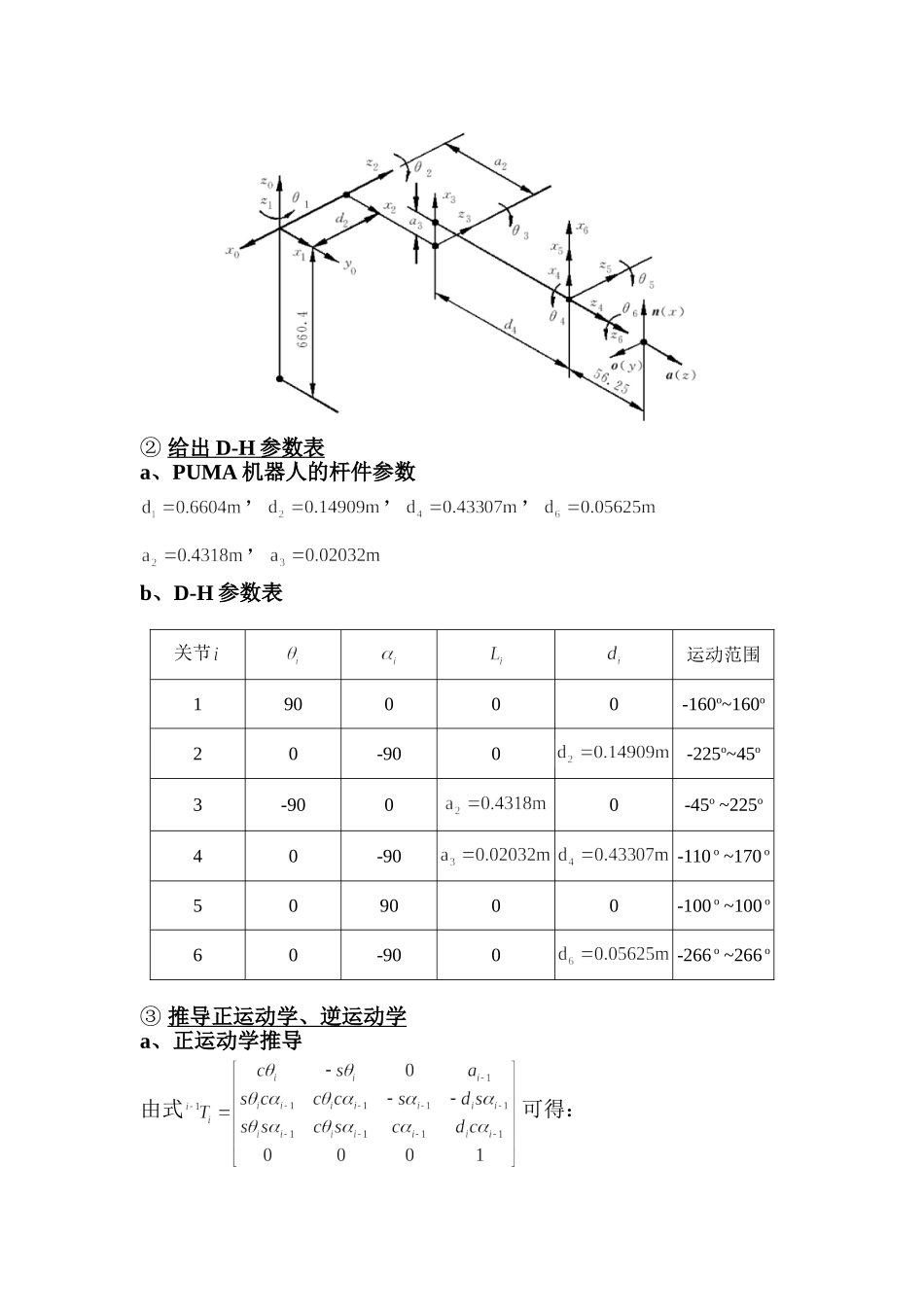
机器人技术课程作业——PUMA机器人如上图所示的PUMA机器人,要求实现右图所示的运动,求解:①建立坐标系;②给出D-H参数表;③推导正运动学、逆运动学;④编程得出工作空间。解:①建立坐标系a、建立原始坐标系b、坐标系简化②给出D-H参数表a、PUMA机器人的杆件参数,,,,b、D-H参数表关节运动范围190000-160o~160o20-900-225o~45o3-9000-45o~225o40-90-110o~170o509000-100o~100o60-900-266o~266o③推导正运动学、逆运动学a、正运动学推导由式可得:由,得机械手变换矩阵:b、逆运动学推导1).求用逆变换左乘方程两边:得三角代换,式中,,得到的解2).求矩阵方程两端的元素(1,4)和(2,4)分别对应相等平方和为:其中解得:3).求在矩阵方程两边左乘逆变换。方程两边的元素(1,4)和(3,4)分别对应相等,得联立,得和和表达式的分母相等,且为正,于是根据解和的四种可能组合,可以得到相应的四种可能值,于是可得到的四种可能解:,式中取与相对应的值。4.求令两边元素(1,3)和(2,3)分别对应相等,则可得只要,便可求出当时,机械手处于奇异形位。5.求根据矩阵两边元素(1,3)和(2,3)分别对应相等,可得6.求根据矩阵两边元素(2,1)和(1,1)分别对应相等,可得从而求得:④编程得出工作空间a、已知条件可以将连杆6的原点做为机器人的动点,连杆6原点相对于坐标系0就是的、、,已知:b、Matlab程序clc,clearlength2=431.8;length3=20.32;d2=149.09;d4=433.07;a=pi/180;fora1=-160*a:20*a:160*afora2=-225*a:20*a:45*aa3=-45*a:20*a:225*afork=1:length(a3)px(k)=cos(a1)*(length2*cos(a2)+length3*cos(a2+a3(k))-d4*sin(a2+a3(k)))-d2*sin(a1)py(k)=sin(a1)*(length2*cos(a2)+length3*cos(a2+a3(k))-d4*sin(a2+a3(k)))+d2*cos(a1)pz(k)=-a3(k)*sin(a2+a3(k))-length2*sin(a2)-d4*cos(a2+a3(k))endplot3(px,py,pz),title('机器人的工作空间'),xlabel('xmm'),ylabel('ymm'),zlabel('zmm')holdongridonendendc、机器人工作空间