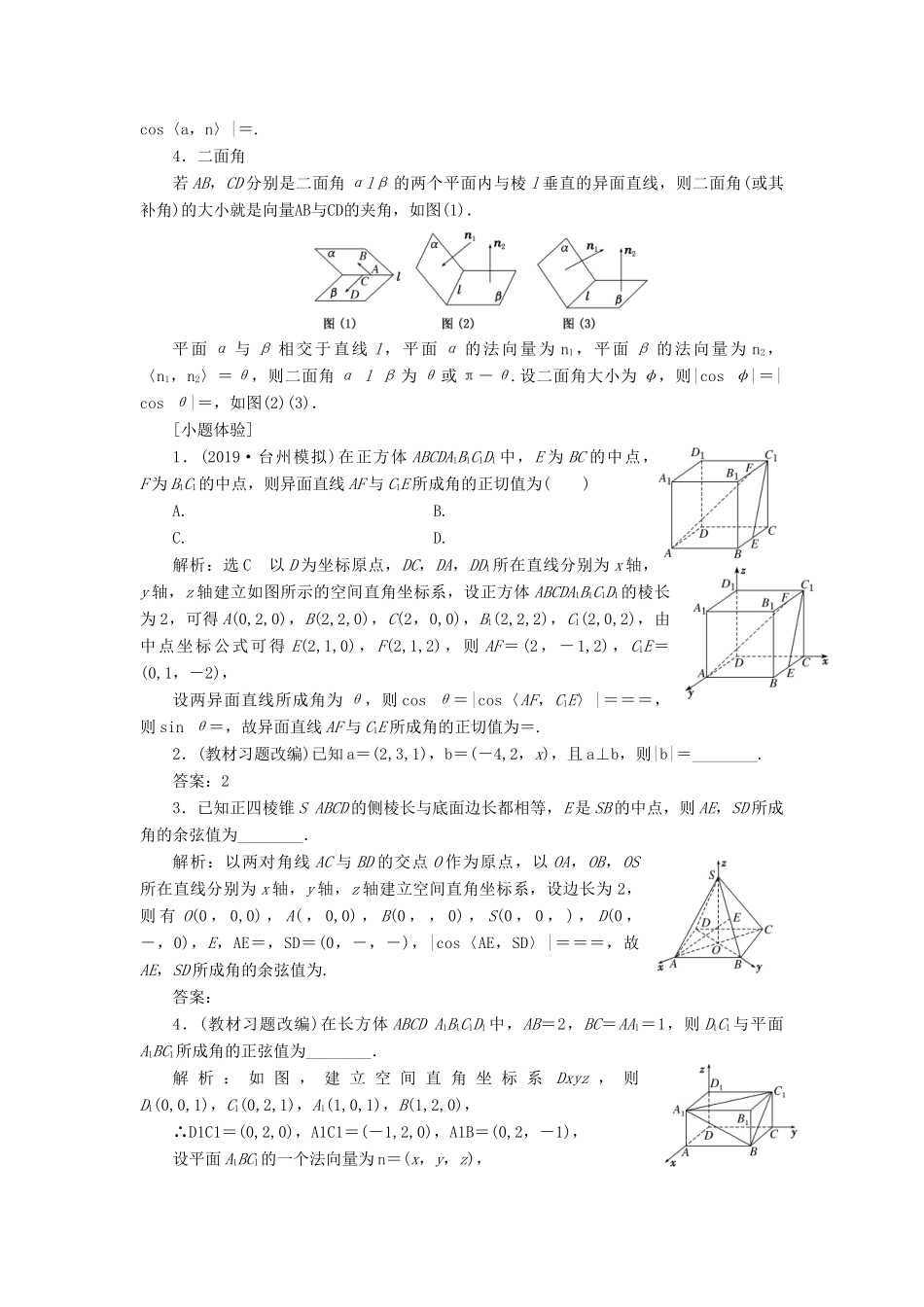
第六节立体几何中的向量方法1.空间向量的概念、数量积及坐标运算(1)空间向量及其相关概念语言描述共线向量(平行向量)表示空间向量的有向线段所在的直线互相平行或重合共面向量平行于同一个平面的向量共线向量定理对空间任意两个向量a,b(b≠0),a∥b⇔存在λ∈R,使a=λb共面向量定理若两个向量a,b不共线,则向量p与向量a,b共面⇔存在唯一的有序实数对(x,y),使p=xa+yb空间向量基本定理定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z}使得p=xa+yb+zc推论:设O,A,B,C是不共面的四点,则对平面ABC内任一点P都存在唯一的三个有序实数x,y,z,使OP=xOA+yOB+zOC且x+y+z=1(2)两个向量的数量积:①a·b=|a||b|cos〈a,b〉;②a⊥b⇔a·b=0(a,b为非零向量);③|a|2=a2,|a|=.(3)向量的坐标运算:a=(a1,a2,a3),b=(b1,b2,b3)向量和a+b=(a1+b1,a2+b2,a3+b3)向量差a-b=(a1-b1,a2-b2,a3-b3)数量积a·b=a1b1+a2b2+a3b3共线a∥b⇒a1=λb1,a2=λb2,a3=λb3(λ∈R,b≠0)垂直a⊥b⇔a1b1+a2b2+a3b3=0夹角公式cos〈a,b〉=2.异面直线所成角设异面直线a,b所成的角为θ,则cosθ=,其中a,b分别是直线a,b的方向向量.3.直线与平面所成角如图所示,设l为平面α的斜线,l∩α=A,a为l的方向向量,n为平面α的法向量,φ为l与α所成的角,则sinφ=|cos〈a,n〉|=.4.二面角若AB,CD分别是二面角αlβ的两个平面内与棱l垂直的异面直线,则二面角(或其补角)的大小就是向量AB与CD的夹角,如图(1).平面α与β相交于直线l,平面α的法向量为n1,平面β的法向量为n2,〈n1,n2〉=θ,则二面角αlβ为θ或π-θ.设二面角大小为φ,则|cosφ|=|cosθ|=,如图(2)(3).[小题体验]1.(2019·台州模拟)在正方体ABCDA1B1C1D1中,E为BC的中点,F为B1C1的中点,则异面直线AF与C1E所成角的正切值为()A.B.C.D.解析:选C以D为坐标原点,DC,DA,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,设正方体ABCDA1B1C1D1的棱长为2,可得A(0,2,0),B(2,2,0),C(2,0,0),B1(2,2,2),C1(2,0,2),由中点坐标公式可得E(2,1,0),F(2,1,2),则AF=(2,-1,2),C1E=(0,1,-2),设两异面直线所成角为θ,则cosθ=|cos〈AF,C1E〉|===,则sinθ=,故异面直线AF与C1E所成角的正切值为=.2.(教材习题改编)已知a=(2,3,1),b=(-4,2,x),且a⊥b,则|b|=________.答案:23.已知正四棱锥SABCD的侧棱长与底面边长都相等,E是SB的中点,则AE,SD所成角的余弦值为________.解析:以两对角线AC与BD的交点O作为原点,以OA,OB,OS所在直线分别为x轴,y轴,z轴建立空间直角坐标系,设边长为2,则有O(0,0,0),A(,0,0),B(0,,0),S(0,0,),D(0,-,0),E,AE=,SD=(0,-,-),|cos〈AE,SD〉|===,故AE,SD所成角的余弦值为.答案:4.(教材习题改编)在长方体ABCDA1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为________.解析:如图,建立空间直角坐标系Dxyz,则D1(0,0,1),C1(0,2,1),A1(1,0,1),B(1,2,0),∴D1C1=(0,2,0),A1C1=(-1,2,0),A1B=(0,2,-1),设平面A1BC1的一个法向量为n=(x,y,z),由令y=1,得n=(2,1,2),设D1C1与平面A1BC1所成角为θ,则sinθ=|cos〈D1C1,n〉|===,即直线D1C1与平面A1BC1所成角的正弦值为.答案:1.共线向量定理中a∥b⇔存在λ∈R,使a=λb易忽视b≠0.2.一个平面的法向量有无数个,但要注意它们是共线向量,不要误认为是共面向量.3.求异面直线所成角时易忽视角的范围而导致结论错误.4.求直线与平面所成角时,注意求出夹角的余弦值的绝对值应为线面角的正弦值.5.利用平面的法向量求二面角的大小时,当求出两半平面α,β的法向量n1,n2时,要根据向量坐标在图形中观察法向量的方向,从而确定二面角与向量n1,n2的夹角是相等(一个平面的法向量指向二面角的内部,另一个平面的法向量指向二面角的外部),还是互补(两个法向量同时指向二面角的内部或外部),这是利用向量求二面角的难点、易错点.[小题纠偏]1.若平面π1,π2垂...