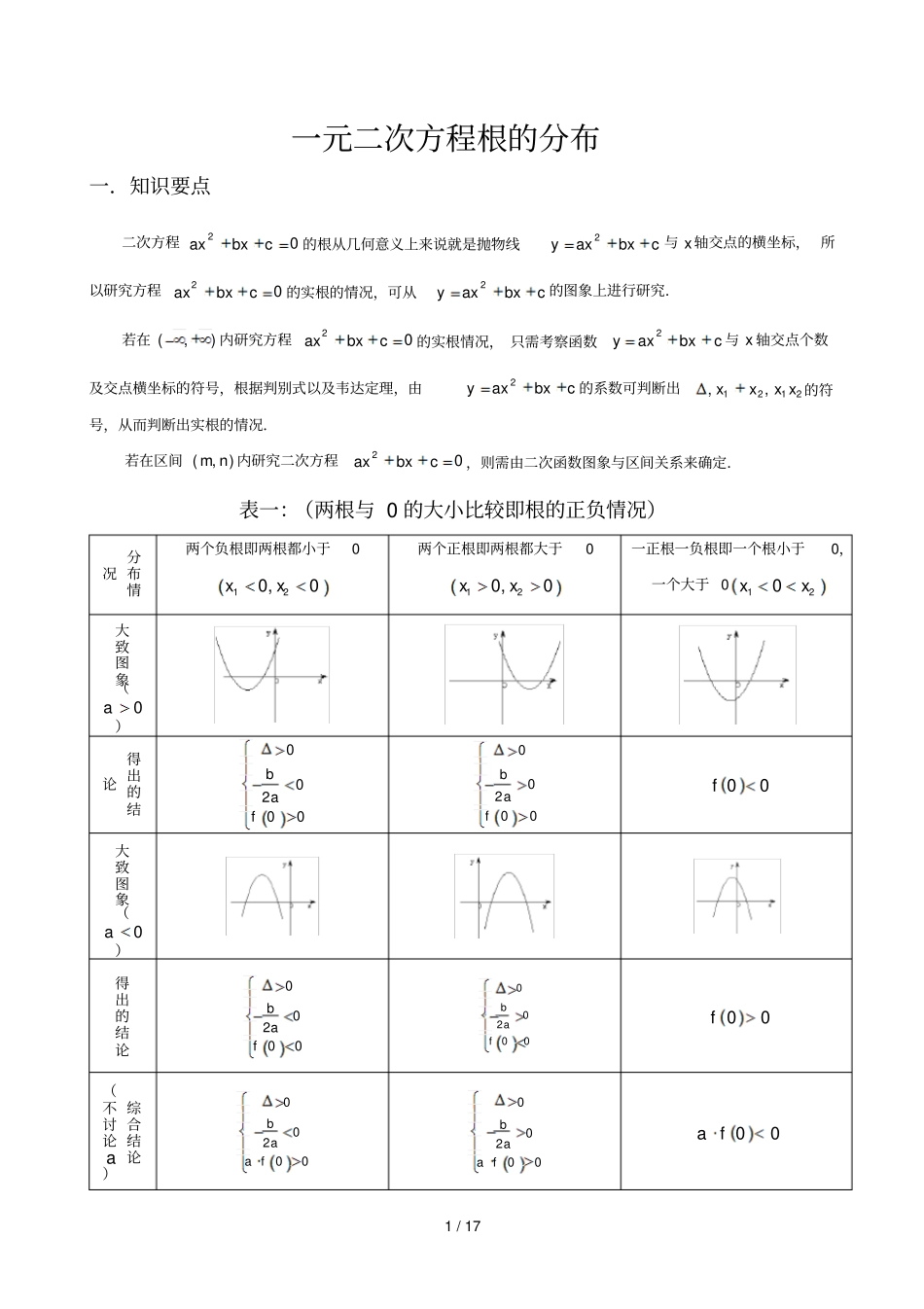
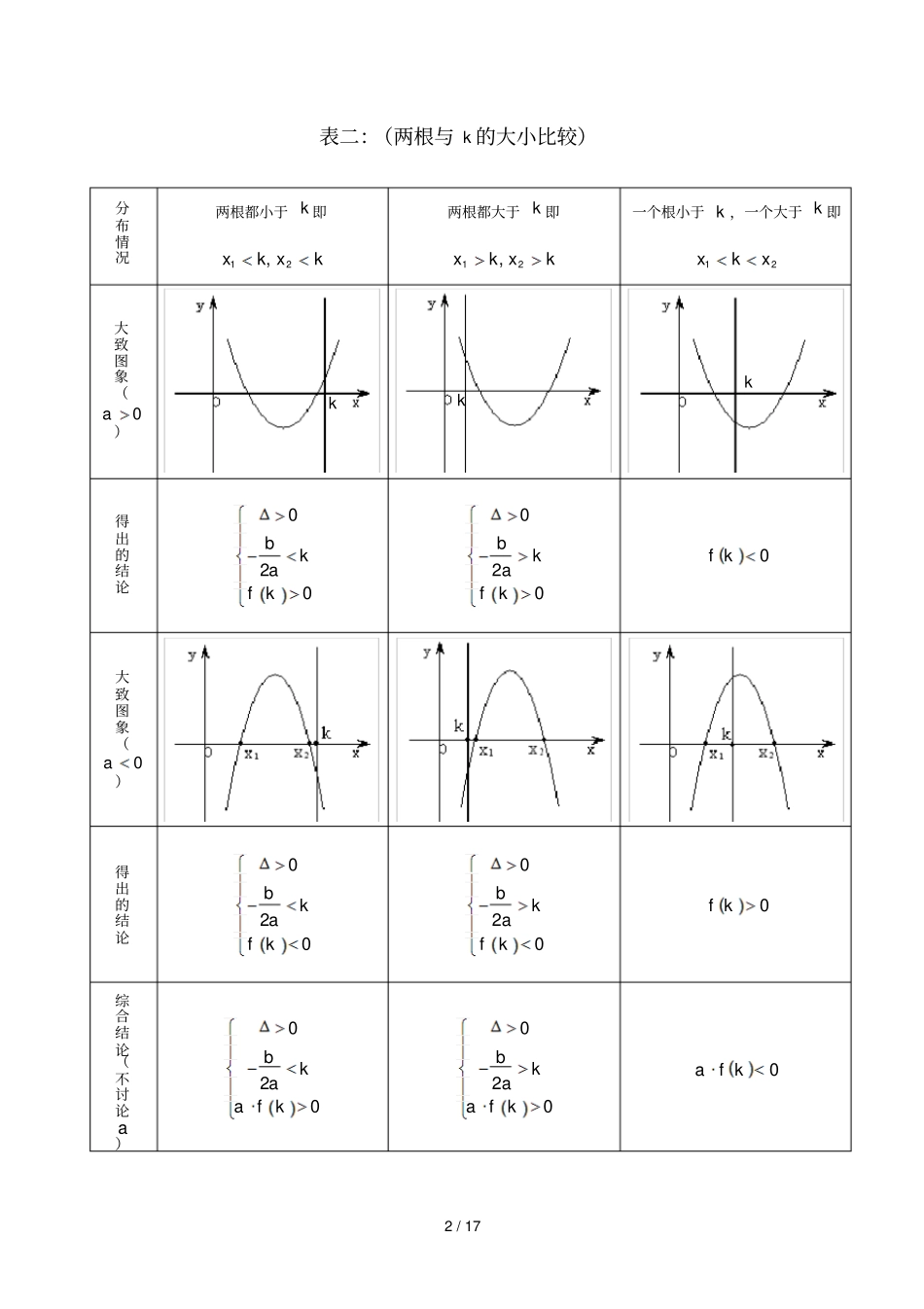
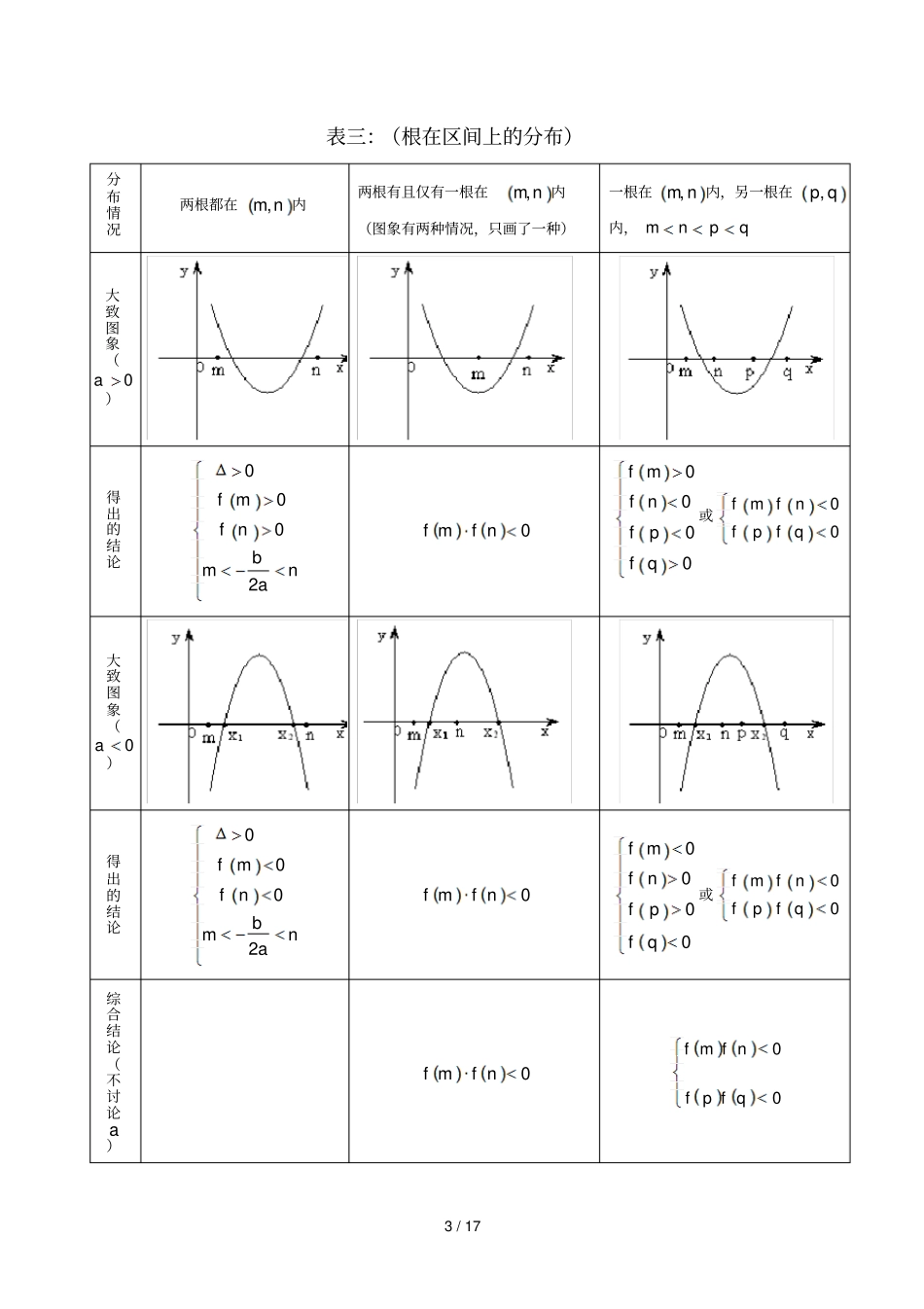
1/17一元二次方程根的分布一.知识要点二次方程02cbxax的根从几何意义上来说就是抛物线cbxaxy2与x轴交点的横坐标,所以研究方程02cbxax的实根的情况,可从cbxaxy2的图象上进行研究.若在),(内研究方程02cbxax的实根情况,只需考察函数cbxaxy2与x轴交点个数及交点横坐标的符号,根据判别式以及韦达定理,由cbxaxy2的系数可判断出2121,,xxxx的符号,从而判断出实根的情况.若在区间),(nm内研究二次方程02cbxax,则需由二次函数图象与区间关系来确定.表一:(两根与0的大小比较即根的正负情况)分布情况两个负根即两根都小于0120,0xx两个正根即两根都大于0120,0xx一正根一负根即一个根小于0,一个大于0120xx大致图象(0a)得出的结论00200baf00200baf00f大致图象(0a)得出的结论00200baf00200baf00f综合结论(不讨论a)00200baaf00200baaf00fa2/17表二:(两根与k的大小比较)分布情况两根都小于k即kxkx21,两根都大于k即kxkx21,一个根小于k,一个大于k即21xkx大致图象(0a)得出的结论020bkafk020bkafk0kf大致图象(0a)得出的结论020bkafk020bkafk0kf综合结论(不讨论a)020bkaafk020bkaafk0kfakkk3/17表三:(根在区间上的分布)分布情况两根都在nm,内两根有且仅有一根在nm,内(图象有两种情况,只画了一种)一根在nm,内,另一根在qp,内,qpnm大致图象(0a)得出的结论0002fmfnbmna0nfmf0000fmfnfpfq或00fmfnfpfq大致图象(0a)得出的结论0002fmfnbmna0nfmf0000fmfnfpfq或00fmfnfpfq综合结论(不讨论a)0nfmf00qfpfnfmf4/17根在区间上的分布还有一种情况:两根分别在区间nm,外,即在区间两侧12,xmxn,(图形分别如下)需满足的条件是(1)0a时,00fmfn;(2)0a时,00fmfn对以上的根的分布表中一些特殊情况作说明:(1)两根有且仅有一根在nm,内有以下特殊情况:1若0fm或0fn,则此时0fmfn不成立,但对于这种情况是知道了方程有一根为m或n,可以求出另外一根,然后可以根据另一根在区间nm,内,从而可以求出参数的值。如方程2220mxmx在区间1,3上有一根,因为10f,所以22212mxmxxmx,另一根为2m,由213m得223m即为所求;2方程有且只有一根,且这个根在区间nm,内,即0,此时由0可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。如方程24260xmxm有且一根在区间3,0内,求m的取值范围。分析:①由300ff即141530mm得出15314m;②由0即2164260mm得出1m或32m,当1m时,根23,0x,即1m满足题意;当32m时,根33,0x,故32m不满足题意;综上分析,得出15314m或1m5/17二.例题选讲(1)两个根在实数k的同一侧例1.已知方程)(0)32()1(242Rmmxmx有两个负根,求m的取值范围.变式1:已知方程2210xmxm有两个不等正实根,求实数m的取值范围。变式2:已知二次方程02)12(2mxmmx的两个根都小于1,求m的取值范围.(2)两个根在实数k的异侧例2:已知二次方程221210mxmxm有一正根和一负根,求实数m的取值范围。变式1:已知二次函数222433ymxmxm与x轴有两个交点,一个大于1,一个小于1,求实数m的取值范围。变式2:求实数m的范围,使关于x的方程062)1(22mxmx.(1)有两个实根,且一个比2大,一个比2小.(2)有两个实根,,且满足410.(3)至少有一个正根.6/17变式3:如果二次函数y=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,试求m的取值范围.(3)在区间),(nm有且只有一个实根例3.已知二次方程22340mxmx只有一个正根且这个根小于1,求实数m的取值范围。变式:已知关于x的二次方程x2+2mx+2m+1=0.若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围.(4)在区间),(nm有两个实根例4:已知关于x的二次方程x2+2mx+2m+1=0.若方程两根均在区间(0,1)内,求m的范围.变式1:已知方程2x2–2(2a-1)x+a+2=0的两个根在-3与3之间,求a的取值范围.变式2:已知方程x2+(3m-1)x+(3m-2)=0的两个根都属于(-3,3),且其中至少有一个根小于1,求m的取值范围.7/17(5)在区间],[nm有实根例5.已知a是实数,函数2()223fxaxxa,如果函数()yfx在区间11,上有零点,求a的取值范围.(6)二次方程实根分布的一些方法除了...