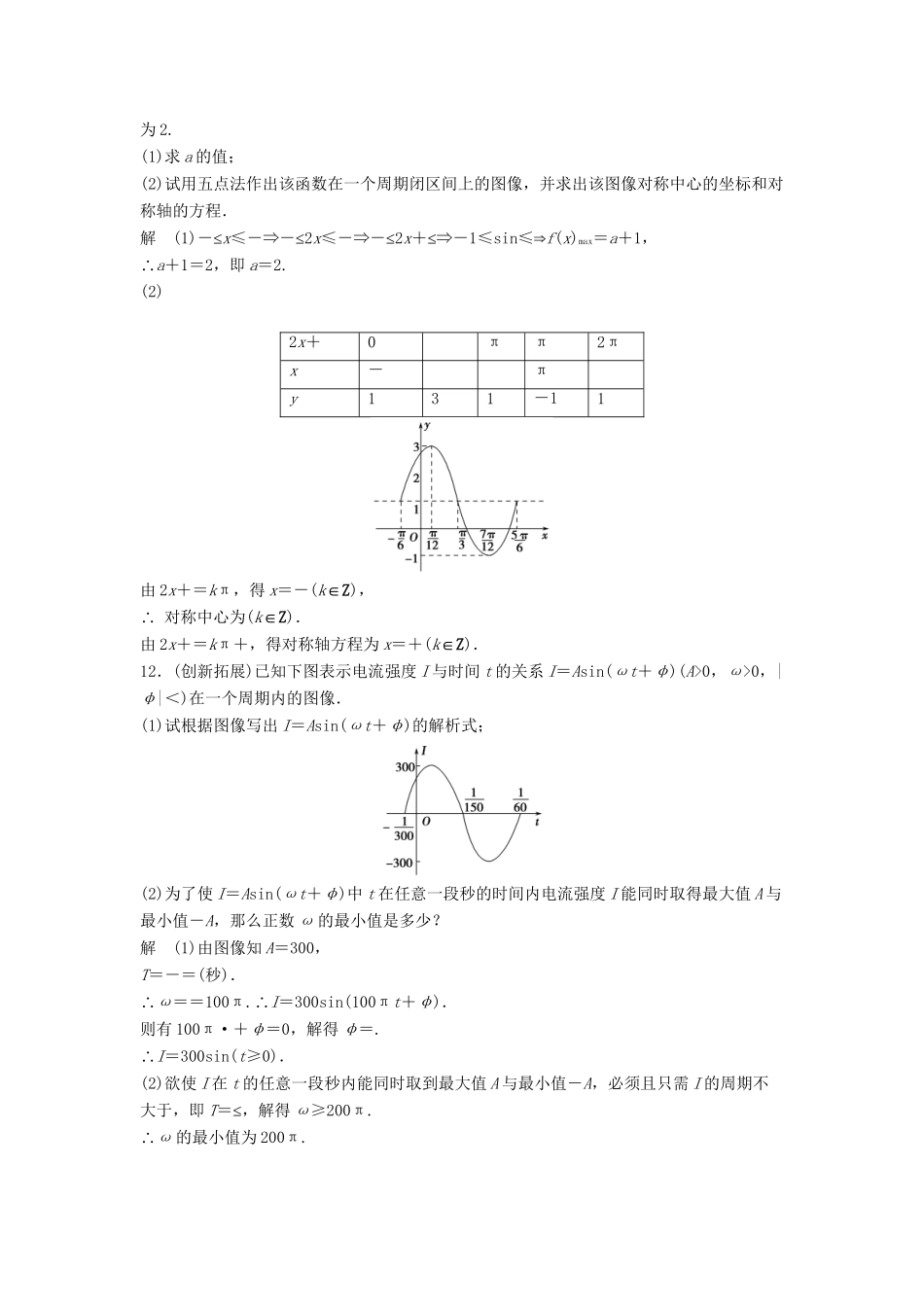
【创新设计】-学年高中数学1-8(二)函数y=Asin(ωx+φ)的图像(二)活页训练北师大版必修4双基达标限时20分钟1.为了使函数y=sinωx(ω>0)在区间[0,1]上至少出现50次最大值.则ω的最小值是().A.98πB.πC.πD.100π解析由题意至少出现50次最大值.即至少需用49个周期,∴49·T=·≤1,∴ω≥π故选B.答案B2.函数f(x)=2sin,当f(x)取得最小值时,x的取值集合为().A.B.C.D.解析令-=-+2kπ,k∈Z,解得:x=4kπ-,k∈Z.答案A3.已知ω>0,0<φ<π,直线x=和x=是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=().A.B.C.D.解析依题意,周期T=2=2π,∴T=,则ω==1.因此f(x)=sin(x+φ).又f=sin=±1,0<φ<π.所以φ+=,∴φ=.答案A4.函数y=sin与y轴最近的对称轴方程是________.解析令2x-=kπ+(k∈Z),∴x=+(k∈Z).由k=0,得x=;由k=-1,得x=-.答案x=-5.已知函数f(x)=2cos-5的最小正周期不大于2,则正整数k的最小值是________.解析由题意,得T≤=2,解得k≥4π,又因为k为正整数,故k的最小值为13.答案136.已知函数f(x)=sin(x∈R).(1)求f(x)的单调减区间;(2)经过怎样的图像变换使f(x)的图像关于y轴对称?(仅叙述一种方案即可).解(1)由已知函数化为y=-sin.欲求函数的单调递减区间,只需求y=sin的单调递增区间.由2kπ≤-2x≤-2kπ+(k∈Z),解得kπ≤-x≤kπ+π(k∈Z).∴原函数的单调减区间为(k∈Z).(2)f(x)=sin=cos=cos=cos2.∵y=cos2x是偶函数,图像关于y轴对称,∴只需把y=f(x)的图像向右平移个单位即可.综合提高限时25分钟7.设函数f(x)=2sin,若对于任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为().A.4B.2C.1D.解析对任意x∈R,f(x1)≤f(x)≤f(x2)成立.∴f(x1)=f(x)min=-2,f(x2)=f(x)max=2.∴|x1-x2|min==×=2.答案B8.如果函数y=sin2x+acos2x的图像关于直线x=-对称,那么a等于().A.B.-C.1D.-1解析法一∵函数y=sin2x+acos2x的图像关于x=-对称,设f(x)=sin2x+acos2x,则f=f(0).∴sin+acos=sin0+acos0.∴a=-1.法二由题意得f=f,令x=,有f=f(0),即-1=a.答案D9.关于f(x)=4sin(x∈R),有下列命题①由f(x1)=f(x2)=0可得x1-x2是π的整数倍;②y=f(x)的表达式可改写成y=4cos;③y=f(x)图像关于对称;④y=f(x)图像关于x=-对称.其中正确命题的序号为________(将你认为正确的都填上).解析对于①,由f(x)=0,可得2x+=kπ(k∈Z).∴x=π-(k∈Z),∴x1-x2是的整数倍,∴①错;对于②,f(x)=4sin利用公式得:f(x)=4cos=4cos,∴②对;对于③,f(x)=4sin的对称中心满足2x+=kπ(k∈Z),∴x=π-(k∈Z),∴是函数y=f(x)的一个对称中心,∴③对;对于④,函数y=f(x)的对称轴满足2x+=+kπ(k∈Z),∴x=+(k∈Z),∴④错.答案②③10.(·江苏)函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图像如图所示,则f(0)的值是________.解析由图可知:A=,=-=,所以T=π,ω==2,又函数图像经过点,所以2×+φ=π+2kπ,令k=0,得φ=,故函数的解析式为f(x)=sin,所以f(0)=sin=.答案11.已知函数f(x)=asin(2x+)+1(a>0)的定义域为R≤,若当-x≤-时,f(x)的最大值为2.(1)求a的值;(2)试用五点法作出该函数在一个周期闭区间上的图像,并求出该图像对称中心的坐标和对称轴的方程.解(1)≤-x≤-⇒≤-2x≤-⇒≤-2x≤+⇒-1≤sin≤⇒f(x)max=a+1,∴a+1=2,即a=2.(2)2x+0ππ2πx-πy131-11由2x+=kπ,得x=-(k∈Z),∴对称中心为(k∈Z).由2x+=kπ+,得对称轴方程为x=+(k∈Z).12.(创新拓展)已知下图表示电流强度I与时间t的关系I=Asin(ωt+φ)(A>0,ω>0,|φ|<)在一个周期内的图像.(1)试根据图像写出I=Asin(ωt+φ)的解析式;(2)为了使I=Asin(ωt+φ)中t在任意一段秒的时间内电流强度I能同时取得最大值A与最小值-A,那么正数ω的最小值是多少?解(1)由图像知A=300,T=-=(秒).∴ω==100π.∴I=300sin(100πt+φ).则有100π·+φ=0,解得φ=.∴I=300sin(t≥0).(2)欲使I在t的任意一段秒内能同时取到最大值A与最小值-A,必须且只需I的周期不大于,即T≤=,解得ω≥200π.∴ω的最小值为200π.