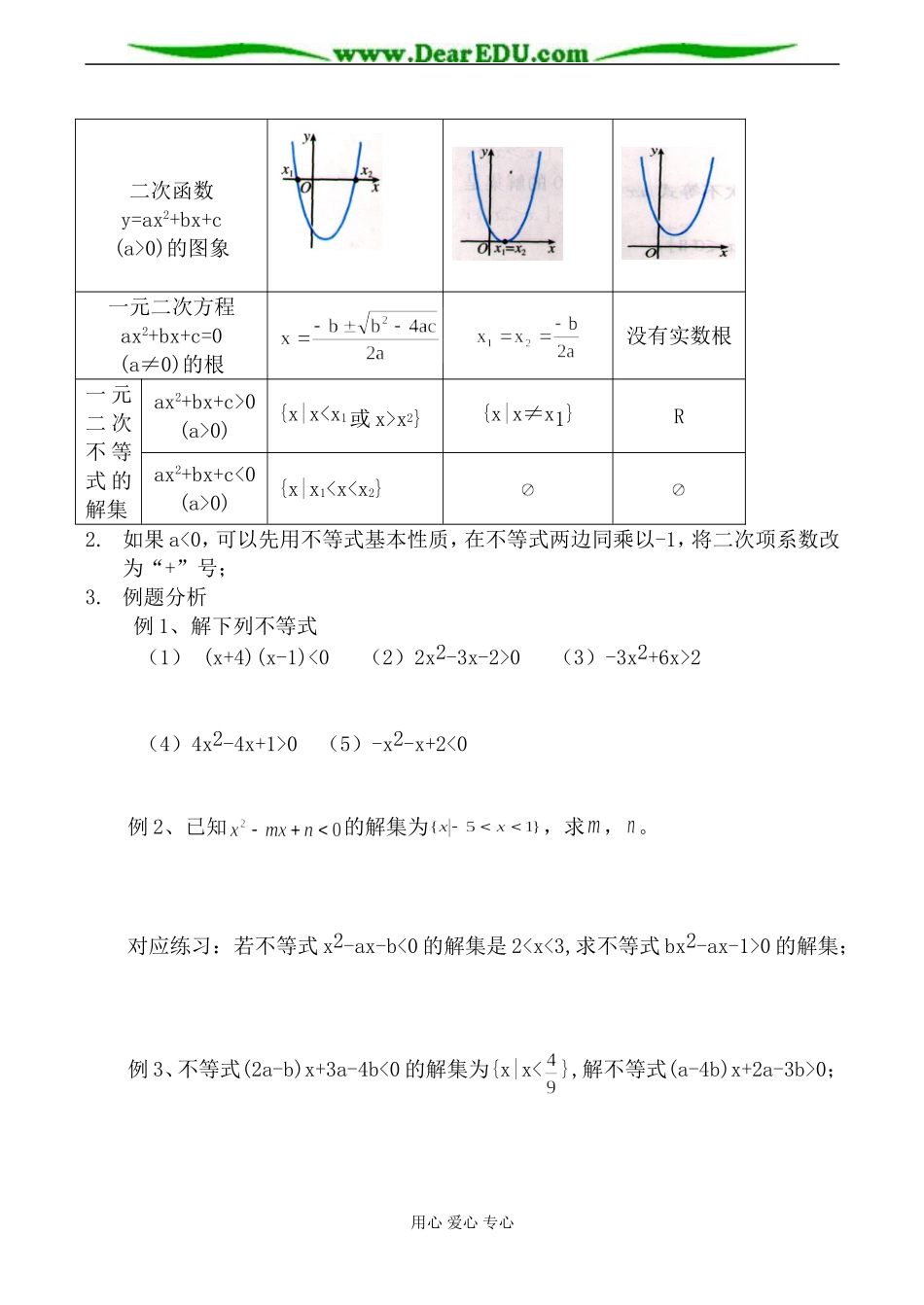
一元二次不等式一、教学目标知识与技能:掌握一元二次不等式的解法;知道一元二次不等式可以转化为一元一次不等式组;了解简单的分式不等式的解法;过程与方法:利用初中学过的一元二次函数图像,引出一元二次不等式的解法。情感与态度:体会知识的前后联系,理解数形结合的数学思想。二、教学过程:(一)引入课题问题1:作一次函数y=2x-7的图象,考虑函数图象与x轴的交点坐标,并思考一元一次方程2x-7=0与一元一次不等式2x-7>0的解之间的联系;问题2:一元二次函数的求根公式?韦达定理?问题3:作二次函数y=x2-x-6的图象,考虑函数图象与x轴的交点坐标,对称轴方程,是否二次函数与x轴一定有交点,判断的标准是什么?问题4:根据图像求出x2-x-6>0与x2-x-6<0的解集?说明:由二次函数的图象可以确定对应的一元二次方程的解和对应的一元二次不等式的解集?(二)新课教学1.对于求一元二次不等式ax2+bx+c>0(a>0)和ax2+bx+c<0(a>0)的解集的问题,我们可以考虑相应的二次函数或一元二次方程的根。一元二次不等式的解法是借助初中学过的一元二次函数的图象讨论它的解集,二次项系数是正数的二次函数、一元二次方程、一元二次不等式的主要结论与三者之间的密切联系如下:判别式△=b2-4ac用心爱心专心二次函数y=ax2+bx+c(a>0)的图象一元二次方程ax2+bx+c=0(a≠0)的根没有实数根一元二次不等式的解集ax2+bx+c>0(a>0){x|xx2}{x|x≠x1}Rax2+bx+c<0(a>0){x|x10(3)-3x2+6x>2(4)4x2-4x+1>0(5)-x2-x+2<0例2、已知的解集为,求,。对应练习:若不等式x2-ax-b<0的解集是20的解集;例3、不等式(2a-b)x+3a-4b<0的解集为{x|x<},解不等式(a-4b)x+2a-3b>0;用心爱心专心例4、解不等式:x2+mx-6m2<0例5,解不等式练习:(1)(2)三,分式不等式的解法(1)(2)练习:(1)(2)(3)已知集合集合,集合,用心爱心专心(1)若(2)若(3)若用心爱心专心