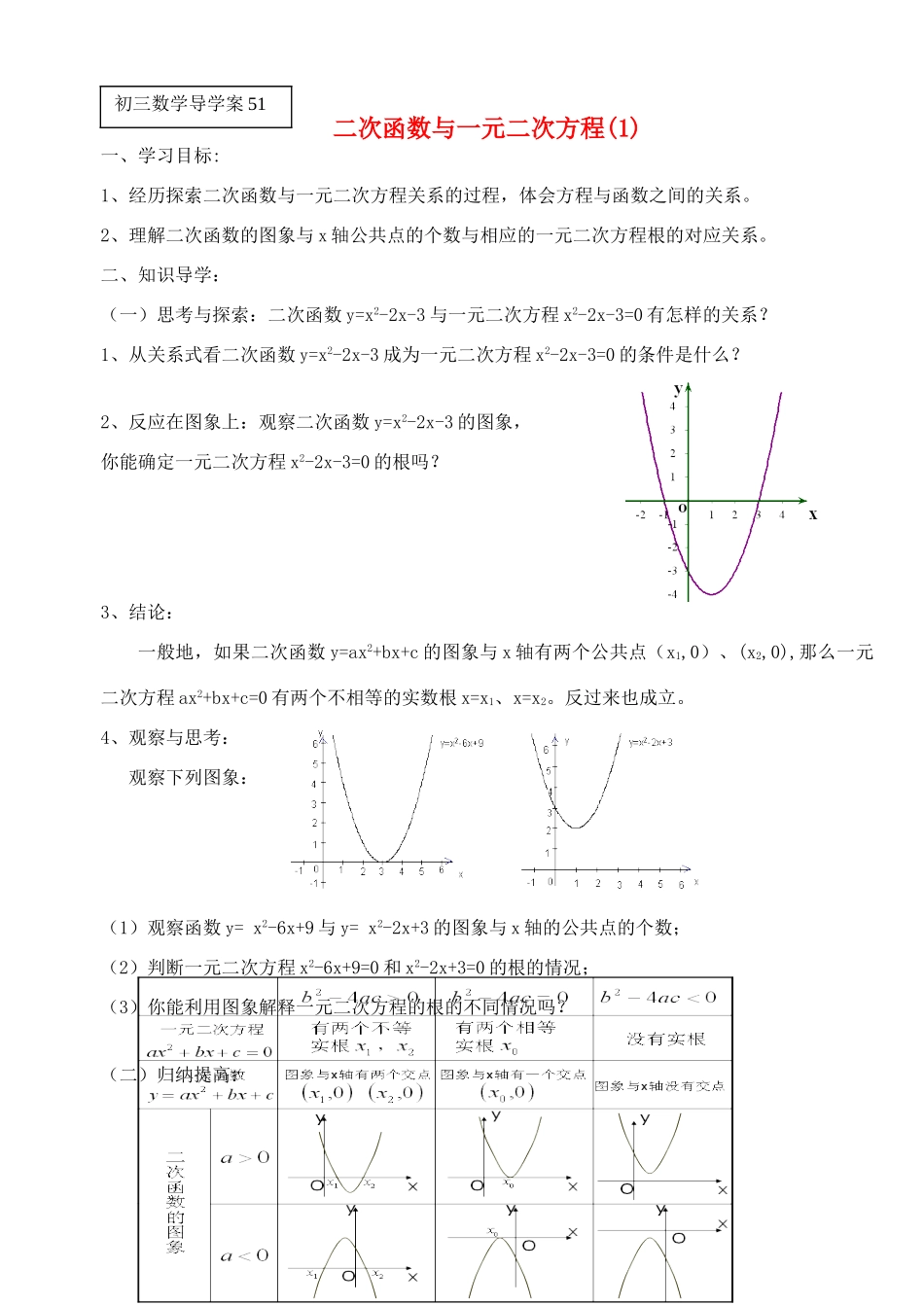
二次函数与一元二次方程(1)一、学习目标:1、经历探索二次函数与一元二次方程关系的过程,体会方程与函数之间的关系。2、理解二次函数的图象与x轴公共点的个数与相应的一元二次方程根的对应关系。二、知识导学:(一)思考与探索:二次函数y=x2-2x-3与一元二次方程x2-2x-3=0有怎样的关系?1、从关系式看二次函数y=x2-2x-3成为一元二次方程x2-2x-3=0的条件是什么?2、反应在图象上:观察二次函数y=x2-2x-3的图象,你能确定一元二次方程x2-2x-3=0的根吗?3、结论:一般地,如果二次函数y=ax2+bx+c的图象与x轴有两个公共点(x1,0)、(x2,0),那么一元二次方程ax2+bx+c=0有两个不相等的实数根x=x1、x=x2。反过来也成立。4、观察与思考:观察下列图象:(1)观察函数y=x2-6x+9与y=x2-2x+3的图象与x轴的公共点的个数;(2)判断一元二次方程x2-6x+9=0和x2-2x+3=0的根的情况;(3)你能利用图象解释一元二次方程的根的不同情况吗?(二)归纳提高:初三数学导学案51(三)例题讲解1、判断下列函数的图象与x轴是否有公共点,说明理由.(1)y=x2-x(2)y=-x2+6x-9(3)y=3x2+6x+112、已知二次函数.(1)当m取何值时,它的图象与x轴有两个公共点?(2)当m取何值时,它的图象与x轴有一个公共点?(3)当m取何值时,它的图象与x轴没有公共点?3、二次函数的图象如图所示,根据图象解答下列问题:(1)写出方程的两个根.(2)写出不等式的解集.(3)写出随的增大而减小的自变量的取值范围.(4)若方程有两个不相等的实数根,求的取值范围.(四)随堂练习:1、方程的根是;则函数的图象与x轴的交点有个,其坐标是.2、方程的根是;则函数的图象与x轴的交点有个,其坐标是.3、下列函数的图象中,与x轴没有公共点的是()4、已知二次函数y=4x+k+2与x轴有公共点,求k的取值范围.5、已知二次函数.试说明此二次函数的图象与x轴一定有两个不同的交点.