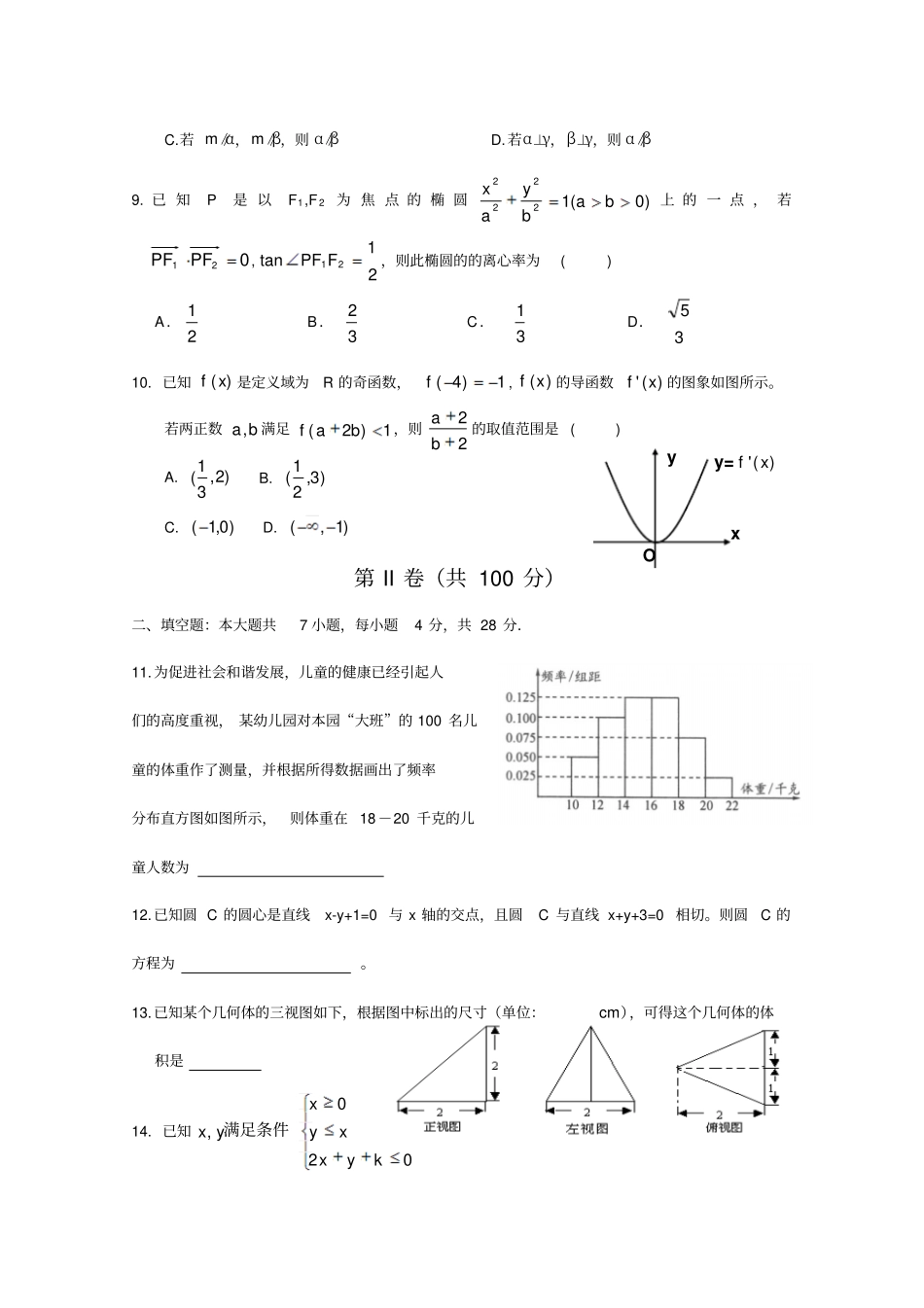
2011年浙江省万全高中数学(文)试卷3一、选择题:1.已知集合{1,2,3,4},{||1|2}ABxZx,则AB()A.{1,3}B.{2,4}C.{1,2}D.{2,3}2.复数22(1)ii等于()A.4B.4C.4iD.4i3.已知,表示两个不同的平面,m是一条直线且m,则“”是“m”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.已知a、b均为单位向量,它们的夹角为60°,那么|a+3b|=()A.7B.10C.13D.45.在等差数列}{na中,若1391197533,100aaaaaaa则的值为()A.20B.30C.40D.506.如图是一个算法的程序框图,该算法输出的结果是()A.54B.43C.32D.217.使f(x)=sin(2x+y)+)2cos(3yx为奇函数,且在4,0上是减函数的y的一个值是()A.3B.35C.34D.328.已知m、n是两条直线,α、β、γ是三个平面,下列命题正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊥α,则m∥nC.若m∥α,m∥β,则α∥βD.若α⊥γ,β⊥γ,则α∥β9.已知P是以F1,F2为焦点的椭圆)0(12222babyax上的一点,若021PFPF,21tan21FPF,则此椭圆的的离心率为()A.21B.32C.31D.3510.已知)(xf是定义域为R的奇函数,1)4(f,)(xf的导函数)('xf的图象如图所示。若两正数ba,满足1)2(baf,则22ba的取值范围是()A.)2,31(B.)3,21(C.)0,1(D.)1,(第II卷(共100分)二、填空题:本大题共7小题,每小题4分,共28分.11.为促进社会和谐发展,儿童的健康已经引起人们的高度重视,某幼儿园对本园“大班”的100名儿童的体重作了测量,并根据所得数据画出了频率分布直方图如图所示,则体重在18-20千克的儿童人数为12.已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切。则圆C的方程为。13.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是14.已知kyxxyxyx020,满足条件Oxyy=)('xfk=.15.分别写1,2,3,4的四张卡中随机取出两张,则取出的两张卡片上的数字之和为奇数的概率是16.在△ABC中,三边a、b、c所对的角分别为A、B、C,若22220abcab,则角C的大小为.17.若对任意x∈R,y∈R有唯一确定的f(x,y)与之对应,则称f(x,y)为关于x,y的二元函数.定义:同时满足下列性质的二元函数f(x,y)为关于实数x,y的广义“距离”:(Ⅰ)非负性:f(x,y)≥0;(Ⅱ)对称性:f(x,y)=f(y,x);(Ⅲ)三角形不等式:f(x,y)≤f(x,z)+f(z,y)对任意的实数z均成立.给出下列二元函数:①f(x,y)=(x-y)2;②f(x,y)=|x-y|;③f(x,y)=yx;④f(x,y)=|sin(x-y)|.则其中能够成为关于x,y的广义“距离”的函数编号是______.(写出所有真命题的序号)三.解答题18.(本小题满分14分)已知A,B,C是△ABC的三个内角,向量)sin,(cos),3,1(AAnm,且1nm.(1)求角A(2)若3sincos2sin122BBB,求Ctan.19.已知数列{}na的首项123a,121nnnaaa,1,2,3,n⋯.(Ⅰ)证明:数列1{1}na是等比数列;(Ⅱ)求数列{}nna的前n项和nS.20.、如图,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,二面角S—CD—A的平面角为45,M为AB中点,N为SC中点.(1)证明:MN//平面SAD;(2)证明:平面SMC⊥平面SCD;(3)若ADCD,求实数的值,使得直线SM与平面SCD所成角为.3021.已知圆C过定点F1(,0)4,且与直线14x相切,圆心C的轨迹为E,曲线E与直线l:(1)()ykxkR相交于A、B两点。(I)求曲线E的方程;(II)在曲线E上是否存在与k的取值无关的定点M,使得MA⊥MB?若存在,求出所有符合条件的定点M;若不存在,请说明理由。22.已知函数1)(2xxf与函数)0(ln)(axaxg.(I)若)(),(xgxf的图象在点)0,1(处有公共的切线,求实数a的值;(II)设)(2)()(xgxfxF,求函数)(xF的极值.温州市五校联考2010-2011年度第一学期参考答案1.C2.A3.B4.C5.C6.B7.D8.B9.D10.B11.1512.22(1)2xy13.343cm14.-615.2316.34(或135)17.②④18.解:(1)因为1mn1623cos3sin1sin()AAAA,所以60A;⋯.7分(2)221sin2cossin3BBB222(sincos)cossin3BBBBsincoscossin3BBBB,85311tantan()tan(60)CABB,所以85311tanC⋯⋯⋯⋯⋯..14分19、解:(Ⅰ)121nnnaaa,111111222nnnnaaaa,11111(1)2nnaa,又123a,11112a,数列1{1}na是以为12首项,12为公比的等...